Bayesian evaluation for the likelihood of Christ's resurrection (Part 34)
Can we quantitatively tackle things like conspiracy theories? What do we do about the interdependency of evidence? One can already imagine the objections to any such attempt. Every assumption would be questioned, and every ridiculous possibility brought up demanding a full numerical treatment. Even if a traditional conspiracy were to be fully debunked in a numerical argument, a skeptic would just weasel the argument to be about a "groupthink induced by religious fervor" instead, and when that got debunked, they would just move on to "have you considered aliens?" Indeed, such weaseling is often the point of bringing up things like conspiracy theories in the first place: not to actually advocate for them, but to make the calculation appear intractable.
But I did say in my last post that I will approach this problem quantitatively - and that's exactly what I'm going to do. Furthermore, my argument will take EVERYTHING into account - government conspiracies, religious groupthink, practical jokes by aliens, everything. Every single possibility for every conceivable degree of evidence dependence will be fully considered.
In addition, empirical evidence will be the foundation of my whole argument. That is, in fact, the key that makes it totally comprehensive. Do you remember the following graph?
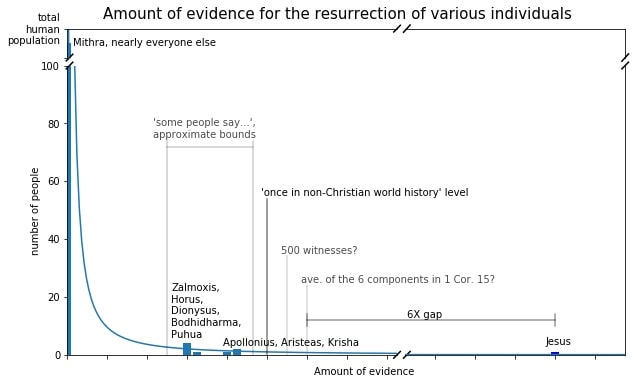
That is the level of empirical evidence that history has actually recorded for the resurrection of various individuals. It's a partial histogram - note the differing number of people with different amounts of evidence for their resurrection. This suggests a probability distribution.
Of course, the graph above isn't the complete record of everyone - it's a small sampling of some people who have the most evidence for their resurrection. But if we had a complete record, we could get a very accurate model for their underlying probability distribution. What would that probability distribution represent?
If we exclude Jesus and the other Christian resurrection reports, the probability distribution we get would be the EXACT model that an empirical skeptic of Christianity MUST use, in predicting the likelihood of a resurrection report. Essentially, the idea is that we can calculate the probability of getting a certain level of evidence for a resurrection, based on how frequently similar reports have come up in history.
Note that, because the raw data is gathered from empirical reports collected in history, this automatically takes things like conspiracy theories into account. The possible interdependency of the evidence is fully included in this model. So you think that a great deal of evidence can be built up through a conspiracy, because the evidence doesn't have to be independent? The distribution includes all such evidence-manufacturing conspiracies that actually existed in history. You want to switch your argument to a religious mass delusion instead? The result of all such mass delusions are also included, at the level of evidence that they actually generated in history.
How about something that has probably never happened in history at all, like an alien resurrecting someone as a joke? Even these possibilities are included, through at least two mechanisms. For one, there are a great many multitude of such unlikely scenarios - and at least one of them might have actually occurred in history, even if a specific one of them was unlikely. So they would have recorded their evidence in aggregate. And secondly, even if such unlikely scenarios never occurred, they can still be accounted for in the modeling of the probability distribution from the samples we actually have. As an analogy, if you were to model people's heights by sampling a thousand people, you will still deduce that human heights follow a roughly normal distribution, and can thereby figure out that there may be someone out there who's at least 7 feet tall, even if such a person was not in your sample.
So you see, this method does in fact take everything into account. It does generate the exact model that an empirical skeptic of Christianity must use. That's the great thing about arguing from empirical, historical records. You can bypass all the difficult and controversial calculations about the probabilities of conspiracies, or the precise degree of dependence among the evidence. All of that automatically gets incorporated into the historical data at their actually correct historical values, and all we have to do is to read off the final result.
Once we have this "skeptic's distribution", the rest of the calculation is fairly straightforward. We can calculate the probability of generating a Jesus-level of resurrection evidence, from the point of view of the skeptic's hypothesis. From a Christian perspective, this probability is within an order of unity, so the skeptic's probability then essentially becomes our Bayes' factor. We then simply see if this Bayes' factor is enough to overcome the low prior probability for a resurrection.
Now, I will use 1e-11 as the prior probability for a resurrection. This is higher than the 1e-22 that I had used earlier - but recall that I only got 1e-22 by simply giving away an additional factor of 1e11 for no reason. I can't afford to just give that away when faced against something as insidious as conspiracy theories. 1e-11 is still smaller than anything that a skeptic can demand based on empiricism, and the rest of the argument will be constructed so that even the minimum Bayes' factor will exceed 1e11. The actual Bayes' factor may exceed 1e22 by the end - I just can't be as precise in my calculations at that level.
We will start constructing this "skeptic's distribution" in the next post.
You may next want to read:
Leave a Reply
You must be logged in to post a comment.
Post Importance
Post Category
• humanities (23)
• current events (27)
• fiction (10)
• history (33)
• pop culture (13)
• frozen (8)
• math (57)
• personal update (19)
• logic (65)
• science (56)
• computing (16)
• theology (101)
• bible (39)
• christology (10)
• gospel (7)
• morality (18)
• uncategorized (2)