Bayesian evaluation for the likelihood of Christ's resurrection (Easter 2020)
This was the state of the "Bayesian evaluation for the likelihood of Christ's resurrection" post, as of Easter 2020. This post will remain unchanged, while the linked post above will have further edits.
I also put up a Facebook post on that date, which is essentially the same as the 2019 Facebook post. The offer mentioned there still stands.
I didn't write an addition to the "epilogue" section this year. I feel like I'm still refining the 3rd draft, but I'm getting more ideas of additional things I can put in. I may have to start pruning all but the very good ideas now. We'll see. Here's to great progress by the next Easter!
Contents:
PART I: The simple version of the argument
Chapter 1: The priors
- The prior odds against a resurrection
Chapter 2: The evidence
- The nature of the evidence for Christ's resurrection
-- The Bayes factor for a human testimony
Chapter 3: Assembling the basic argument
- Is the evidence enough?
- There is far more than enough evidence to overcome the prior
PART II: Double checks
Chapter 4: Double checking our evaluation of human testimonies
- Why are we double checking? What are we double checking?
- Double check: the Bayes factor of a human testimony.
-- The frequency of lies
-- Car accidents
-- Human death
-- LinkedIn claim
-- Fake 9/11 victims
-- One red dot in a million
-- One in a million events happen every month
-- Video of a lottery winner
-- Summary of the findings
-- The strength of a human testimony is firmly established and understood.
-- The first step in a testimony: the inception of the idea
-- The "human honesty" step, and dependence factors in multiple testimonies
Chapter 6: Double checking against the other resurrection reports in history
- Can naturalistic explanations account for the resurrection testimonies?
-- Well, can you demonstrate that empirically?
- The New Testament, and what it would take to match its resurrection reports
-- Peter, James, Paul
-- Apollonius of Tyana
-- Zalmoxis
-- Aristeas
-- Mithra
-- Horus and Osiris
-- Dionysus
-- Krishna
-- Bodhidharma
-- Puhua
- Our previous calculations are fully validated
PART III: Answering simplistic objections
Chapter 7: The usual barrage of objections
- What, if anything, is wrong with the previous argument?
-- Is the prior too large, especially for a supernatural event?
-- "But Science!"
-- Can human testimonies be trusted?
-- Can the New Testament be trusted?
-- Could the disciples have been genuinely mistaken?
-- Or actively deceptive?
-- Or actually crazy?
-- Or some combination of the above, or something else entirely?
Chapter 8: The strength of a Bayesian argument: why none of these objections work
- The nature of Bayesian arguments.
PART IV: Addressing all possible alternatives
Chapter 9: Time to address the crackpot theories
- The next steps
- Examining crackpot theories, in general
Chapter 10: The "skeptic's distribution".
- Using the historical data to construct the skeptic's distribution
-- Assigning numerical x values
-- What should be the form of this "skeptic's distribution"?
-- Details of the distribution: generalized Pareto distribution and its parameters
-- But how should we determine the value of the shape parameter?
-- Defining "outliers"
-- Back to determining the shape parameter
- The alternate hypothesis and its distribution
- Empirical evidence from other historical figures in ancient history
-- The Buddha
-- Confucius
-- Socrates
-- Tiberius
-- Arguments using the New Testament itself
- The exact mathematical form of the "Christian's distribution"
-- The robustness of the Christian's distribution
-- Simulation and code: The number of "outliers" decides the case.
-- Putting Jesus's resurrection over the top: the list of outliers
Chapter 13: Tuning the "ratio of distributions" approach
- We were far too generous for the "skeptic's distribution"
-- The power law distribution
-- The boundaries of outliers
-- A better estimate of the probability
- Defenses against crackpot theories built in to Christianity
-- Apostle Paul
-- The "final" odds for the resurrection
PART V: More double checks
Chapter 15: Double check: reports of miracles in other religions
- The stance on non-Christian miracles
- Ichadon
- Vespasian
-- "Something happened" vs. "a miracle happened"
- Splitting the Moon
- Accounts in Josephus
-- Honi the Circle-drawer
-- Eleazar the exorcist
-- "Something happened" vs. "a miracle happened", again
Chapter 16: Double checks for the "ratio of distributions" approach
PART VI: Challenge and conclusion
Chapter 17: The final challenge: replicate the results
- The rationale for this challenge
Chapter 18: Conclusion and epilogue
- Conclusion
more ideas:
go straight into the strongest argument for 1e8 being the strength of a human testimony?
rewrite section to fully describe the complexity of human trustworthiness, or at least very explicitly say so. - switch chapters 4 and 5.
shorten the summary of the strength of a human testimony bayes factors examples?
better priors? the general relativity argument takes care of that
independence investigation: get into the mind of individuals.
- coin flips for fair/double heads: still dependent because of truth itself. So it should still affect things even for Paul's independence.
- demonstrate that order of consideration of facts don't matter
- how does reward/risk/effort change that?
check end
The prior odds against a resurrection
What is the probability that Jesus rose from the dead?
Here I'm going to construct a rather foolish partner to advance certain arguments. This is just a rhetorical device. I have to be careful to not commit a straw man here, nor do I wish to insult anyone. I don't intend to imply that anyone actually thinks like my partner. But while he's too foolish to actually stand in for any specific person, he can therefore be useful, by standing in as the lower bound on what a reasonable person may think. Please just understand him as the artificial rhetorical construction that he is.
Now, my foolish partner may say, "the probability that Jesus rose from the dead is zero. What's there to talk about?" But by doing so, he has committed the cardinal sin in Bayesian reasoning. Any real, non-theoretical probability CANNOT be absolutely zero or one. Think about what a zero probability value means: this represents a state of mind where absolutely NOTHING - no amount of possible evidence - can alter their beliefs. There is no reasoning with such a person.
I am very certain that the sun will rise tomorrow. I may be 99.9999...% certain, but I cannot be 100% certain. That tiny difference between 99.9999...% and 100% represents possibilities like a super-advanced alien race stopping the rotation of the earth, or me being momentarily confused about what is meant by "the sun". And I am not 100% certain, because I can, at least in theory, be shown evidence that such an alien race exists, or that I had momentarily confused "the sun" with "the north star".
My partner may then say, "well, the probability may not be actually zero, but it's very close to it. Like, 0.000.....001%. Nobody has ever come back from the dead before." But actually, isn't that the very thing we're talking about? Whether Jesus had come back from the dead? Furthermore, it's presumptuous to think Jesus was just like everyone else, that he wasn't special in any way. Even if nobody else came back from the dead, we would need to do some additional thinking in the case of Jesus.
My partner would reply, "see, that's just special pleading. I don't see why Jesus should be special. Empirically, people do not come back from the dead. Therefore it's also highly unlikely that Jesus came back."
At this point, I'm going to simply give away the point about whether Jesus was special or not. I obviously believe that he was - but quite frankly, the argument for the resurrection is so strong that I can just handicap myself in several different ways like this without materially affecting the conclusion. I'll be doing this multiple times throughout this post.
Now, back to how many people came back from the dead, "empirically": how many different people have you seen die and stay dead? Remember, we're talking about "empirical" evidence here, meaning that we only count people that you, yourself, have seen die in person. For many people, that number is probably zero. It might be one or two - maybe you've seen a grandparent pass away. Maybe more, if you're a healthcare worker or something like that.
My partner may say, "Even if I didn't see someone die in person, if there was a real resurrection, it would be all over the news. And there hasn't been any such reports, because people do not rise from the dead."
Well, at this point, my partner is begging the question on whether there has in fact been such reports, and is becoming slippery about what "empirically" means. But again, I will simply handicap myself and give away these points. "Empiricism" in the sense of "I only believe what I can see" is fundamentally flawed, anyway (It's self-defeating). So let's adopt a more reasonable form of empiricism, and say that news reports are enough, and a direct observation is unnecessary. So, how many people have been covered in the news that you've seen? Thousands? Millions? If the argument is that Jesus was no different than these thousands or millions of other people, then I freely acknowledge that this does in fact establish an upper bound on the probability of the resurrection. However, this does NOT prove that the probability is zero, no more than a dozen coin flip of heads proves that the coin will always land heads. Instead, it merely says that the probability for the resurrection is likely to be below a certain level.
For example, say that you've examined a thousand swans, and they all turned out to be white. You want to use this fact to investigate the existence of a black swan. Now, your study of a thousand white swans don't prove that black swans are an impossibility, with a probability of zero. Instead, it impose a prior probability against a report of a black swan: there is only somewhat less than 1/1000 chance that the reported swan is actually black. If you've instead examined a million swans that were all white, then your probability of observing a black swan would correspondingly drop to around 1/1 000 000 as the upper limit. (For the technically minded: I'm starting with the Jeffreys prior of Beta(1/2, 1/2), then adding in the number of observed "white swan" events to approximate the "black swan" probability distribution. This is standard practice.)
Now, the modern media is pretty comprehensive, so my partner may say, "The world news covers many millions of other people. And none of them have come back from the dead. So the chance that Jesus came back from the dead is, at best, one in a million. That's basically zero. How could you believe in something that has only one in a million chance of being true? That's irrational."
Well, one in a million is a pretty small probability. But actually, I think we can just go ahead and say that out of the entire world population of 8 billion people, none of them are going to be raised from the dead. So, the probability for the resurrection has now dropped to 1 in 8 billion. I'm just giving away everything here. I've almost dropped the condition about an "empirical" probability. I'm making a blanket statement that absolutely nobody in the world, independent of anything that may be know about them, will rise from the dead. So, if we apply this general "observation" to the likelihood of Jesus's resurrection, that probability must be below 1 in 8 billion.
My partner may respond, "Um... So now you're making my argument for me. So yeah. The probability of the resurrection is less than 1 in 8 billion. Obviously you can't believe in something that unlikely to be true. This is why any naturalistic explanations must always be preferred to a supernatural one in these discussions of miracles, because the supernatural is always so unlikely."
Oh, but I'm not done yet. I'm going to give away even more of the argument. Why not just drop all pretense of an "empirical" probability? Why not say that everyone who has EVER lived - about 100 billion people in total - have all died, without a single one of them being raised from the dead? Forget saying anything about "empirical observations". Forget any semblance of reasoning from our direct experiences. Ignore anything about reported resurrections. I will simply grant that every single one of these 100 billion people have died and stayed dead. And against the weight of those 100 billion people, we'll estimate the probability of Jesus's resurrection. According to our previous line of thinking, this puts that probability at 1 out of 100 billion.
My foolish partner may say, upon the strength of this evidence that I have made up for him, "One in a hundred billion! Do you know how unlikely that is? That's 1 out of 100 000 000 000. That's a probability value of 0.000 000 000 01. That's basically zero. Just concede the argument - it's virtually impossible that Jesus rose from the dead. Absolutely any naturalistic explanation is going to be more likely than that."
Well, should I just concede? That does seem like a very impressive number, no? How did we even get to this point? I started with the "Nobody rises from the dead, so Jesus also didn't rise from the dead" argument. I then stretched it to its strongest form, to include the entire current world population. I ignored all objections about the specifics in Jesus's case, or the exact meaning of "empiricism". But all that wasn't enough - I wanted it to be stronger still. So I then added some made-up stuff on top, to strengthen it even further, to a level beyond any possible empirical justification.
So now, as it stands, the probability of Jesus actually having risen from the dead is 1 out of 100 000 000 000 - essentially zero. That's game over, right? How could I, or anyone, believe in something so unlikely to be true? How could any hypothesis with a probability of 0.000 000 000 01 ever be taken seriously?
"Um... so yeah. What are you doing?", my partner may ask.
You'll see. Read on, and you'll behold and understand the power of evidence.
The nature of the evidence for Christ's resurrection
That probability value for the resurrection - 0.000 000 000 01 (which can be written as 1e-11, employing scientific notation) - is a prior probability. That is, it's a probability based on the background information, taking into consideration the fact that Jesus was human, and that humans don't rise from the dead.
However, it is just the starting point. To proceed from this point on, let us first consider some scenarios - they may seem like a detour, but we'll be back on track soon enough.
Let's say that you're meeting someone new. You talk for a while, and the conversation turns to birthdays. You reveal that you were born in January, and your new friend says, "Oh, really? I was born in January too!" He seems earnest - he's not obviously joking, sarcastic, or ingratiating. From the little you know of him, he's not any more likely to be delusional or deceptive than anyone else.
Now, based only on his earnest word, would you be willing to believe that your new friend really was born in January? Note that I'm not looking for 100% certainty here. A willingness to entertain the idea, to give it a 50-50 shot of being true, is all that's required.
Also note that I'm not asking whether this event is likely to happen. Obviously, the probability that you and a random other person shares the same birth month is about 1/12, so it may be said to be "unlikely". Rather, I'm asking whether you would believe this person, given that this unlikely event has already occurred.
So, how would you respond? Would you say, "I find your claim to be highly dubious. There's only 1/12 chance that you were born in the same month as me"? Or would you simply reply, "Oh, hey, that's neat!"
I'm going to assume that you're willing to believe your new friend. I think you'll agree that it takes a special kind of jerk to say "I don't believe you. You must be lying or mistaken. It's just too unlikely for us to share the same birth month". In that case, what if it had turned out that you share the exact same birthday? You mention that you were born January 23rd, and he claims the same. Would you still believe him?
Now let's tweak the scenario a bit: what if he learns the birthdays of everyone in your family, and then claims multiple matches? Say that you had written down a list of these family birthdays, and your new friend happens to come across it. He then says, "hey, we share the same birthdays - and our moms do too!" Would you believe him? And what if he had made the claim for the first three people on the list - you, your mom, and your dad?
At what point does such a claim become too unlikely for you to believe? If your friend had made the "shared birthdays" claim for the first four, five, or six people on your list - siblings, grandparents, cousins - at what number would you have said "I cannot believe this - this is too unlikely to be true", in spite of your friend's sincere and insistent claim?
Decide on an answer, and remember it. Write it down somewhere. We'll come back to this answer soon. Make a firm statement like, "I would be willing to believe up to 3 shared birthdays - myself, mother, and father - but if he claimed 4 or more I would begin to be skeptical".
Let's try another example. Let's say that you run into an acquaintance whom you haven't seen in a while. You exchange greetings and ask how he's been, and he excitedly tells you - "Guess what! I've actually won the jackpot in the lottery last month! I'm rich!" As before, he seems earnest - he's not obviously joking, sarcastic, delusional, or deceptive. Would you believe him, based only on his earnest word? Again, only a willingness to entertain the idea, just granting a 50 - 50 chance of it being true, is all we're looking for here. Would you give him at least even odds that he's telling the truth?
And if you would, how about if he claimed to have won two consecutive jackpots? How about three? At which point would you say "That's just too much for me to believe"?
Next, let's switch over to other gambling games. Say that a friend claims to have had a very lucky night at the card tables. He says that he got a royal flush in a 5-card stud poker game. Would you believe him? What if he claims to have gotten two royal flushes last night? What if he claims three? At what point would you say, "I don't believe you. You seem earnest and all, but the chances of that happening are just too small"?
How about if he were playing Texas Hold'em, and claims to have had multiple pocket aces? Say that he claims to have had two, three, four, or five pocket aces last night. At what number does it become too unlikely to be true, despite your friend's sincere claim?
We can ask similar kinds of questions in many different ways. What if someone claims to be born naturally as a part of twins, triplets, quadruplets, or quintuplets? What if someone claims to have recently been struck by lightning? Or that they were a victim of two or three such strikes?
Remember, in all these cases, that we're not looking for certainty. Just a willingness to entertain the idea - a 50-50 likelihood for the statement is true - is enough to say that you'd believe your friend. Also, we're not asking whether these scenarios are likely; rather we're asking if you'd continue to believe this earnest person, despite the fact that he's claiming that an unlikely event happened.
Answer these questions. Give a specific number in each case: we want answers like "four royal flushes" and "two lightning strikes". Write them down somewhere - we'll come back to them later.
Now, we'll turn to the question of Jesus's resurrection.
The Bayes factor for a human testimony
Recall that we had rather generously put the probability against Jesus's resurrection at a prior value of 1 out of 100 billion (that is, 0.000 000 000 01, or 1e-11). At such extreme values, "probability" is nearly synonymous with "odds": so the prior odds against Jesus's resurrection is 1e-11.
Recall also that this was only the starting point. It does not take into account any evidence we have specifically about Jesus's resurrection. Remember Bayes' rule: the final, posterior odds is the prior odds times the Bayes factor, which is the ratio of the likelihoods of each hypotheses generating the evidence. So the number we have now is just the prior odds. We now need a numerical value for the Bayes factor of the evidence, and then we can get our posterior odds.
But what kind of evidence is there for Christ's resurrection? And how could it possibly overcome a prior odds of 1 to 100 000 000 000 against it? Well, as for the evidence, we have the writings of the New Testament, where Jesus's resurrection and his follower's testimonies are documented. Okay, but is this "evidence" any good? How can we put numerical likelihood ratios to these things?
What we need is the numerical strength of a human testimony, of the type that Jesus's disciples gave. As it turns out, we can actually get a not-unreasonable, order of magnitude estimate of this value. Remember your answers to the probability questions in the previous section? I hope you have them written down or otherwise recorded, because we will use them to calculate the Bayes factors that you would personally assign to a human testimony that's making unlikely claims.
Let's use my personal answers, given below, as an example for how to do these calculations. These are my gut answers to the questions, before doing an actual probability calculations. Remember, "believe" here means that I'm willing to give at least even odds (50/50 chance) on the claim. It doesn't mean certainty, and it doesn't mean that I'd stop looking for more evidence. It only points to how much I'm willing to adjust my beliefs based on someone saying "yes, I know it's unlikely, but it really happened".
For the shared birthday question, I would easily believe that my friend shared a birthday with me. I would also not have any real problem believing that our mothers also shared birthdays. At three people - myself, mother, and father - I would start becoming skeptical, but would probably give my friend the benefit of doubt. Starting with four shared birthdays in the family, I would start leaning more heavily towards skepticism.
On winning the lottery, I would not really doubt that my friend won the lottery. I would start doubting if he says that he won two consecutive lotteries.
On getting a royal flush, I think I could almost believe that my friend got two such hands in a very lucky night at the table. I feel like three would be entering the realm of the fantastical, and I would doubt my friend at around this number.
On pocket aces, I would be willing to believe that my friend had up to four or five pocket aces in a lucky night of Hold'em.
On the multiple births, I would not have any real problems believing that someone was a part of natural quadruplets. A claim to be in a quintuplet would start to cause a little bit of doubt to me, and a claim of sextuplets would need additional evidence.
On being struck by lightning, I actually had someone around me claim that this had recently happened to her. I had no problem believing it. Even if she had claimed two such accidents I don't think I would have really doubted her. If she had claimed three, I would start to be skeptical.
Now, calculating the numerical probability values for all these things is pretty straightforward:
The probability of sharing a single birthday is 1/365, or 1/3.65e2. The probability of sharing the three birthdays for your family is then simply this number cubed - 1 in 4.86e7.
The probability of winning the lottery varies by exactly which lottery you're talking about, but the odds for the jackpot are generally somewhere around 1 in 1e8.
The probability of getting a single royal flush is 1 in 6.5e5. The probability of getting two in two hands is therefore this number squared, 1 in 4.2e11. We can then take it down by a couple orders of magnitude, to account for the fact that there's dozens of hands played in a poker night. That gives us something like 1 in 1e9 for the odds.
The probability for getting pocket aces is 1 in 221. Getting five would then be 1 in 5.3e11. Taking it down again by several orders of magnitude to account for multiple hands, that brings us to something like 1 in 3e7.
The probability of natural quadruplets is about 1 in 1e6, and for quintuplets it's about 1 in 5.5e7. We'll split the difference here and call it 1e7.
The probability of getting struck by lightning in a given year is about 1 in 1e6. If we count "recently" as the last 5 years, that would bring it down to 1 in 2e5. Getting struck twice would then be 1 in 4e10, then maybe take off an order of magnitude for possible dependency factors to give us 1 in 4e9.
So, looking at the final numbers above - 1/4.9e7, 1/1e8, 1/1e9, 1/3e7, 1/1e7, 1/4e9 - we seem to be getting a reasonably consistent estimate for how I value the strength of an earnest, personal testimony. There are a lot of small details we can go over again (how many hands of poker did you play last night? Is your friend someone likely to play the lottery, or to be outdoors during a thunderstorm?), but these will largely be random, small, unknowable effects that will get washed out in this order-of-magnitude calculation.
So, we'll take the geometric mean of the above values(1/1.3e8), and then conservatively round down to get 1/1e8, or 1e-8, as their "average" probability. In other words, even if an event had only a 1e-8 prior chance of happening, I would be willing to give even odds on that event having occurred based on someone's earnest, personal testimony.
So such a testimony will shift the odds from 1/1e8 to 1/1. Or, to put it yet another way: the typical Bayes factor for an earnest, personal testimony about an unlikely event is around 1e8. That is my numerical value for the strength of a human testimony, under the conditions specified above.
It is important to note that this number is not something that I just made up. The math that gives this value is described above in its entirety. What answer did you get when you plugged in the numbers? That is the number that you, personally, must be willing to assign to the strength of a personal testimony, if you are to be consistent. I believe that most reasonable people will be within a couple of orders of magnitude of my answer.
Double checking the Bayes factor: Lottery winner
Now, we don't want to just take someone's personal answers and simply run with it - even if that someone is ourselves. It's also possible for a sufficiently hardheaded skeptic to simply say "I won't believe anything that anyone tells me". For these reasons, it's important to double check our answers with empirical evidence, and to correct any mistakes we've made. Fortunately, there are a number of different ways to do that.
Consider this thought experiment: some time in the future, you find yourself telling someone, "I just hit the jackpot in the lottery". You are being sincere and insistent. Now, what is the probability that you're telling the truth here?
Again, the odds of winning the lottery is about 1e-8. So if you agree with my assessment that personal testimony should be valued at a Bayes factor of around 1e8, then you are about equally likely to be telling the truth or lying in this scenario. However, if you disagree with that assessment - for example, if you think that personal testimony should only be valued at 1e6 - then you're saying that the posterior odds of you having won the lottery is still only 1/100, and so you're 99% likely to be lying in that scenario. Which is it?
And what if we were to expand this to people beyond yourself? Imagine investigating a random sample of people who claimed to have won the lottery. Remember, we're only counting earnest, insistent, personal claims to the jackpot. What fraction of them are telling the truth? How many of them are actual lottery winners? If you say "maybe around half?", then you're agreeing with my Bayes factor of 1e8. If you want the Bayes factor to be 1e4 instead, then you need 99.99% of these people to be liars. Meaning, you need to find me 10 000 liars for every true winner I can find.
Well, fortunately for us, this "lottery liars" experiment has actually been naturally conducted, and we can compare its result with our numbers. On January 13, 2016, the Powerball lottery produced the largest jackpot in history (as of the time of this writing): 1.6 billion dollars. This jackpot ended up being split three ways. But - were there people who lied about having won this jackpot? As a matter of fact, there were. Several people on social media claimed to be a winner, presumably in an attempt at some quick, cheap fame. How many such people were there?
I couldn't get an exact number for the number of Powerball jackpot liars, but we can still get a sense, an order-of-magnitude estimate. Snopes, for example, mentions two people by name, and "several" or "numerous" others. Another report claims "a number" of similar hoaxes. So - it sounds like maybe ten people lied about winning the jackpot? It's certainly not in the hundreds or thousands.
How does that compare with the estimates from my probability calculation? Well, the odds of hitting the jackpot in Powerball are about 1/3e8. However, people may buy multiple tickets - which many people certainly did on such a well-publicized jackpot. In the end, there were 3 actual winners, out of the total American population of 3e8 people. So the prior odds for a specific person in the United States being a winner was 3/3e8, or 1/1e8.
Now, if the Bayes factor for an earnest personal testimony is 1e8, then the posterior odds is just the product of 1/1e8 and 1e8, which is 1. That translates into 1 actual winner for every liar. So, given that there were 3 actual winners to the jackpot, we should expect around 3 liars - and that is roughly what we actually appear to have, within an order of magnitude.
You can again nitpick at this example (the great publicity of this jackpot, the people who made an earnest claim offline, the relative certainty of a short-lived notoriety for lying, etc.) But as an order-of magnitude estimate, the results of this natural experiment are about as good as I can possibly hope for.
We get similar results from other similar calculations: for instance, the Bayes factor for someone claiming a rare and extraordinary position on LinkedIn has a Bayes factor distinctly above 1e7. And a report of a sudden tragic death can be demonstrated to have a Bayes factor around 1e8. And an entirely different approach, used to calculate the Bayes factor of the specific kind of individual testimony found in the New Testament, gives us a Bayes factor of more than 1e9. We will later return to these and many other calculations in great detail. They are all in agreement with our current line of thought, and so they all validate one another.
But for now, let us proceed with the rest of the basic Bayesian argument, using 1e8 as the typical Bayes factor of the kind of testimony we're concerned with. It is certainly not several orders of magnitude less than that.
Is the evidence enough?
Now that we have all the necessary numerical values, we can finally calculate the probability that Jesus rose from the dead.
To begin, I gave the prior odds for Jesus's resurrection as 1e-11. This number was obtained from the argument that "empirically, people do not rise from the dead. Therefore, Jesus also couldn't have risen from the dead." I took that argument, then made it as strong as possible, then gave away everything that it asked for, then gave away even some more things that it didn't ask for, to the point of strengthening it beyond all bounds of empiricism. This number is equivalent to a prior obtained by individually checking and confirming that every single person who has ever existed has failed to resurrect. In other words, this 1e-11 is a smaller odds than anything that any skeptic can reasonably ask for.
Next, we calculated a typical value for the Bayes factor for the relevant kind of testimony - a seemingly earnest, sincere, personal testimony, making an unlikely claim. It worked out to be about 1e8. It's certainly not much less than that.
Now, we simply apply Bayes' rule: posterior odds are prior odds times Bayes factors (the likelihood ratio). So, we'll just look through the New Testament, and see if we can find people who made an earnest, personal claim that Jesus rose from the dead. Let's start in 1 Corinthians 15, because that's a famous passage on the resurrection, recognized even by skeptical scholars as originating within a few years of Jesus's death. It's a good partial summary of the other resurrection-related testimonies in the New Testament. It reads:
For I delivered to you as of first importance what I also received: that Christ died for our sins in accordance with the Scriptures, that he was buried, that he was raised on the third day in accordance with the Scriptures, and that he appeared to Cephas, then to the twelve. Then he appeared to more than five hundred brothers at one time, most of whom are still alive, though some have fallen asleep. Then he appeared to James, then to all the apostles. Last of all, as to one untimely born, he appeared also to me.
So, who in this passage can be said to have made an earnest, personal claim of Jesus's resurrection? Well, there's Cephas, also known as the apostle Peter. He's a major character in the New Testament, and every one of the numerous accounts of him says that he did, in fact, testify that Jesus rose from the dead. Certainly, that's one witness. The odds of Christ's resurrection after taking Peter's testimony into account is now 1e-11 * 1e8 = 1e-3.
Anyone else we can find here? Well, there's Paul, the author of the very text we're reading, and one of the most prolific writers of the New Testament. He himself says in this passage that the risen Christ appeared to him. Furthermore, Paul was initially a dedicated opponent of Christianity, before his miraculous conversion. So barring some crackpot conspiracy theories, there's little worry about any strong dependency factors which would significantly reduce the impact of his testimony. In fact, his testimony could naturally expect to be anti-correlated with Peter's, but let's just ignore all that. We'll count his testimony at a Bayes factor of 1e8. The odds of Christ's resurrection after taking it into account is now 1e-3 * 1e8 = 1e5, or 100 000 to 1 FOR the resurrection.
Huh, would you look at that. After taking just two witnesses into account, the odds are now in FAVOR of the resurrection. And this is literally using just a fraction of the first passage we chose in the New Testament! Even within this passage, we still haven't taken into account James, or the other members of the twelve disciples, or the other apostles, or the five hundred that are mentioned. And then, we still have the rest of the New Testament to still go through!
What happened? The prior odds was 1e-11 - that's 1 in 100 000 000 000! Wasn't that supposed to be an impossibly small odds? Wasn't it suppose to be insurmountable? Wasn't it something that enabled atheists to simply say, "therefore any naturalistic explanation is bound to be more likely"? Wasn't it a bulwark for skepticism, based on some kind of empiricism? How could it have just... evaporated like that?
That is the power of evidence. Evidence can cause swings in probability that seem ridiculously large to people who are not actually familiar with the mathematics. Did you think that a billion is a large number, or that a probability of one in a billion is too small to ever care about? It is not. In some kinds of math, even numbers like a googol (1e100) can disappear to nothing in just a few lines of calculation. And probability is one example of that kind of math.
Just the other day at my work (Bayes' theorem and probability calculations are part of my day job), a Bayes factor of 1e-10 came up. It merited no comment beyond "that's pretty small". Another time, 1e-40 appeared as a Bayes factor, again with little commentary on its magnitude. Numbers like that are not atypical in probability calculations. Do you realize that, if I specify the order of cards in a shuffled deck of playing cards, that I'm doing so against an odds of 1 to 8e67? That if I hand you a record of a chess game (which can fit on a single post-it note), I'm specifying one out of at least 1e120 possibilities? So, a billion - which is only 1e9 - is not a large number. And the prior odds against the resurrection - which is only 1e-11 - gets completely blown away when it's set against the evidence.
Here, it's important to again note that I'm handicapping the argument for the resurrection. I already mentioned how the prior odds of 1e-11 was far smaller than anything that a skeptic can reasonably ask for. As it turns out, the Bayes factor of 1e8 for a personal testimony is also smaller than it could have been. It's the right value for our general case, but in specific situations it may be far larger. Note the above example of recording a chess game: if you choose to believe that my record of the game is accurate, you're giving me a Bayes factor of around 1e120 for my testimony.
So, as it stands for the moment, the odds are around 100 000:1 in FAVOR of the resurrection, using only Peter and Paul's personal testimonies. The seemingly strong "nobody rises from the dead, so Jesus couldn't either" argument has been fully overcome, with only a tiny fraction of the evidence we have in the New Testament. At this point, the resurrection is already quite probable - but I suppose we might as well finish off the passage we've started on, to see how the odds grow from here.
From here, I'm going to be pretty sloppy for the rest of this calculation, because it just does not matter in the end. The case for the resurrection is just that strong. In particular I'll be setting aside some kinds of crackpot theories for now, which allows me to ignore some kinds of dependence factors. We will address those points more fully later. But for now, this won't affect our conclusion - we're just piling more evidence on top of an already near-certain proposition with the remaining testimonies in 1 Corinthians 15.
So, let's see who else comes up in 1 Corinthians 15. There's James, the brother of the Lord. He's another major character in the New Testament, another major player in early Christianity. We have no doubt that he professed that Jesus rose from the dead. So that's an additional named witness. Taking his testimony into account, the odds of Christ's resurrection is now 1e5 * 1e8 = 1e13 for the resurrection.
Furthermore, 1 Corinthians 15 says that Jesus appeared to "the twelve", and also to "all the apostles", which form two distinct groups. Let's first consider "the twelve". To compute their Bayes factor, we'll go ahead and cut down their number to include only the better-known disciples who are mentioned more often in the New Testament. Say that leaves us with 4 disciples. With some dependency factors and all, let's give each of these disciples a Bayes factor of 100 for their testimony. That value represents a rather low opinion of their trustworthiness: you wouldn't believe such a person even if they told you their own birthday.
Even so, the overall Bayes factor for "the twelve" is still 100^4, or 1e8. If we also give "all the [other] apostles" the same Bayes factor, the odds of Christ's resurrection, after taking these two groups into account, now becomes 1e13 * 1e8 * 1e8 = 1e29.
1 Corinthians 15 also mentions Jesus appearing to "more than five hundred brothers at one time". It's clear that Paul had a specific set of people in mind, as they are part of this early central creed, and Paul mentions that some of these people have died. The number 500, too, is not something anyone just made up - it seems as if the passage is extra careful to mention that some have died, because this may have reduced the actual number of living witnesses to below 500. But let's just ignore all that. Let's pretend that Paul (and the early Christians) exaggerated this number by a factor of ten, so that there were only 50 people claiming to have seen the resurrected Christ. Let's furthermore give them a Bayes factor of 1.5 for their testimonies - meaning you wouldn't trust them to report their own gender correctly. Again, even with these low values, their overall Bayes factor is 1.5^50, which is still well over 1e8. The odds of Christ's resurrection, after taking these people's testimonies into account, is now over 1e29 * 1e8 = 1e37.
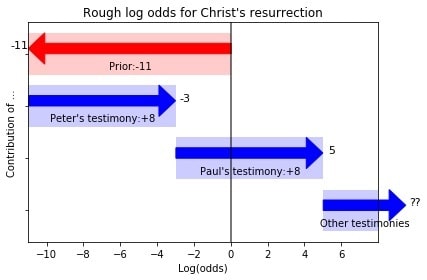
Now, as I said there's a lot of sloppiness in the above calculation. The dependency factors need to be handled more carefully, and one should be careful of making claims with numbers like 1e37 as the actual, final odds in a real-world context, for at those levels even the crackpot conspiracy theories can come into play. But really, the fact that we have to even worry about that is a testament to the strength of the evidence. We will come back to all these points later - but what IS completely clear, even at this early point, is that the evidence for the resurrection completely overwhelms the prior odds. Jesus almost certainly rose from the dead.
There is far more than enough evidence to overcome the prior
This brings us to the end of the 1 Corinthians 15 passage. We can go through the remainder of the New Testament, but that'd be lot of work to improve an odds that's already near certainty - so this is a good place to stop for now. What have we achieved? Consider:
We have only used the strength of personal testimonies. That is, we've only used the fact some people have said that they have personally witnessed to the resurrected Christ. We have not yet taken into account any other kinds of evidence, such as the fulfillment of Old Testament prophecies, or physical facts like the currently empty tomb, or historical facts like Christianity's explosive early growth, or anything else.
We have used conservative numbers in each step of our calculations.
We have only focused on a single passage from the entire New Testament.
We have only considered a rather weak version of a human testimony, like someone being earnest in a single meeting. But the disciples did much more - they were sincere, insistent, and enduring in proclaiming the resurrection, for the rest of their changed lives. Most of them died as martyrs - for making the same claim, with the same earnest seriousness, to everyone they would meet. This elevates their testimony to a whole new level, which we have not accounted for.
And even under these restrictions, the testimonies have easily overcome the 1e-11 prior odds against a resurrection, and have reached posterior odds corresponding to near certainty. If I were to carry out a more complete and reasonable calculation, using all the different lines of evidence that a modern Christian has at his or her disposal, the final odds would further increase still, by multiple orders of magnitude. Jesus almost certainly rose from the dead.
Questions about Bayes rule and human testimony
My claim, at its heart, is very simple: the evidence of the many people claiming to have seen the risen Christ is abundantly sufficient to overcome any prior skepticism about a dead man coming back to life. My argument consists of backing up that statement with Bayesian reasoning and empirically derived probability values.
The emphasis on empirical values is important. Humans are notoriously bad at estimating probabilities, especially when the values reach extreme levels, like 1e-11. Some people, especially when discussing a controversial topic like the resurrection, will just pull their numbers out of thin air. They'll make statements like "I'll grant a 23.599% chance that the disciples went to the wrong tomb". This can sometimes result in some pretty hilarious statements, like someone assigning a 1% chance for a generic conspiracy theory - as if they couldn't imagine anything less likely than a 1% probability.
This is why having an empirical basis for the probability values is crucial. Otherwise, you're likely to simply make up such worthless numbers, influenced only by your preconceived notions. In my argument, none of the numbers I used are something I just made up. They each have empirical backing.
The two important numbers are the prior odds for the resurrection, and the Bayes factor for a human testimony. I set the prior odds at 1e-11: this is, as I said, far more conservative than any requirement of empiricism. There is no way to argue that it should be set lower, although that won't stop some people from abandoning empiricism as soon as it conflicts with their preconceived notions. We'll deal with such arguments in due time.
As for the Bayes factor of the relevant kind of human testimony, I've set it at 1e8. I've given some empirical evidence that this is the correct value, and will provide much more in the chapters to come. But before we get to that, let me acknowledge that this number may be difficult to accept or understand. Many people are more comfortable with probabilities. Bayes factors are a less intuitive, less familiar concept. This is unfortunate, as Bayes factors are crucial to understanding and evaluating evidence. In fact, the logarithm of the Bayes factor is an excellent mathematical translation of what we mean by "the amount of evidence".
There are two ways compute a Bayes factor. The first is from its definition: the ratio of the likelihoods, where the likelihood for a hypothesis is the probability of it generating the evidence in question. In this way, the hypotheses are judged relative to one another, by how well they explain the evidence.
The second way is to compute the Bayes factor from what it does: it moves the odds for the hypothesis. Remember Bayes' rule: posterior odds is prior odds times the Bayes factor. So, if you would change your mind dramatically upon learning of a new piece of evidence, that piece of evidence should have an enormous Bayes factor. The odds of a random person having won the lottery jackpot is very low, but the odds among those who seriously claimed to have won is very much higher. Therefore, that claim of having won the lottery must be accorded a very high Bayes factor.
We can use either method to calculate the Bayes factor, and we will use both in the future to verify our calculations. But before we do so, we should address any niggling doubts you may still have about quantifying human testimony in this way. Maybe these doubts are not exactly about Bayes rule or the value of the Bayes factor, but about some other surrounding issues on which you feel a cloud of uncertainty. You may feel, for example, that 1e8 still somehow gives too much credit to human honesty. Or that 1e8 is too much at odds with the Bayes factor of 1e120 for a chess game record. Since both are a form of human testimony, you may worry that such a large difference points to a flaw somewhere. Or perhaps you're disturbed by how much the Bayes factor for a testimony seems to be influenced by the prior probability of it being true. Or maybe, you're not sure how to stack multiple testimonies together. The math is easiest if the testimonies are independent - you just multiply the Bayes factors - but of course, this almost never happens in reality. So how do we take all these into account?
Answering these questions involves digging deeper into what makes up a human testimony - which we will now do.
The first step in a testimony: the inception of the idea
I'm thinking of a false statement right now. Can you guess what it is?
You almost certainly cannot. There are so many possible false statements out there - a functionally infinite number - that to be able to guess the specific one that I'm thinking of is basically impossible. For instance, the false statement could have been "I played this specific game of chess last night", accompanied by a random chess game record. The odds against guessing that are at the best 1e-120. There was essentially no way for that specific statement to get into your head.
This illustrates an important point in evaluating a claim from human testimony. The thought for a claim, whether it's a truth or a lie, first has to somehow get into the human's head. Then afterwards, they may choose to make the claim or not. Each of these two steps are conditioned on whether the claim is true or false, and the overall Bayes factor for the claim will depend the combination of both steps.
Let's go through a specific example, again of a chess game. Say that you watch a game and record it, and present the following as the game record:
1. e4 e5 2. f4 exf4 3. Bc4 Qh4+ 4. Kf1 b5 5. Bxb5 Nf6 6. Nf3 Qh6 7. d3 Nh5 8. Nh4 Qg5 9. Nf5 c6 10. g4 Nf6 11. Rg1 cxb5 12. h4 Qg6 13. h5 Qg5 14. Qf3 Ng8 15. Bxf4 Qf6 16. Nc3 Bc5 17. Nd5 Qxb2 18. Bd6 Bxg1 19. e5 Qxa1+ 20. Ke2 1-0
Now, if this record is in fact the truth, then how did it get into your head? Well, that's easy - it's the truth, you watched it happen, and you recorded it as it was happening. The probability this game record entering your head, if it really did happen this way, is near certainty.
But what if the game did not in fact happen this way? Well then - it's something of a mystery how you even thought to record this other, incorrect game. Why this specific game record, out of more than 1e120 possible untruthful chess games? The chance of this specific game record even entering into your head in the first place is at most 1e-120, if it were chosen at random.
Then the Bayes factor for the truthfulness of this game record is at least the ratio of the two numbers above - "near certainty" at 1, and 1e-120 - resulting in 1e120. This is just based on the fact that the record even entered into your mind at at all, and before you make any actual claims about whether the record is in fact true. It happens simply as a matter of the regular operation of a human brain, and quite independently of how honest you are.
The "human honesty" step, and dependence factors in multiple testimonies
The next step in the process, after the game has first come into your mind, is to make the actual claim based on what's in your head. Because people are usually honest, you are more likely to make the claim if it's the actual truth, and less likely to make the claim if it's false. This adds an additional Bayes factor for the truthfulness of the game record, but this factor is generally small - much smaller than 1e120. The exact value varies by individuals and circumstances, but something like 1e2 may serve as a guess here. In other words, people tell the truth about 99% of the time (as a guess), when the truth and the falsehoods are both present in their minds.
This explains why some may feel that numbers like 1e8 or 1e120 are somehow too large to be the Bayes factors for a human testimony. They're intrinsically thinking of something like 1e2 as the proper Bayes factor, for a scenario where someone has both a truth and a lie as fully present alternatives in their minds. This may be the proper number if someone merely gave a reply under direct questioning - as in "did you, or did you not, see the defendant at the scene of the crime?" This is the proper Bayes factor if someone flips a coin and tells you that it landed heads. It's the kind of number that intuitively comes to mind when you're asked to assess "human honestly". But it is incorrect for the kind of voluntary, declarative claims made by the earliest Christians announcing Jesus's resurrection.
This also illustrates the effect of dependency factors in how multiple testimonies stack together. The first testimony, presenting new information, should be given a large Bayes factor like 1e8. A second testimony should be given something much smaller, like 1e2, if it only assents to the correctness of the first testimony. Further testimonies offering only confirmations would get ever smaller Bayes factors, but a new, independent testimony would get the full value again.
The "stretchiness" of human testimony
Now, let's throw a twist into the example. Your game record above turns out to be identical to that of the Immortal Game - arguably the most famous chess game in history. What are we to make of that? How does it change the Bayes factor for that game record?
It drastically reduces it, of course. Recall that the enormous Bayes factor exceeding 1e120 came mostly from the first step, where we assumed that a specific incorrect game record had less than a 1e-120 chance of randomly getting into your head. Well, as a very famous chess game, the Immortal Game would not have been selected randomly. Even if that wasn't the actual game that was played, it could have entered into your head in a number of different ways, all of which are much more plausible than 1e-120. This precipitously drops the Bayes factor. So, there's essentially no chance that your game record is correct, right?
Actually, this has far less impact on the final, posterior odds than you might guess. One may think, "Oh, so you're saying that a random chess game someone played just happened to be the exact replication of the most famous chess game ever? Give me a break!" But this was unlikely to be a random chess game, from the beginning. As one of the most famous games ever, the Immortal Game has a much, much higher chance of being played than a random, 1 out of 1e120 game. The game you witnessed may have been an exhibition match from a series of famous historical matches. Or you may have simply gone to an online chess site which replays famous games. Or the two players may have planned out the game beforehand as a demonstration, stunt, or a joke.
So, the Bayes factor of your game record becomes much smaller than 1e120, but the prior odds of that game actually being played becomes much greater than 1e-120. In fact, the two effects will cancel out to a significant degree. A moment's reflection reveals why: the same mechanism is responsible for both effects. A famous game is more likely to be replicated in actual play than a random game. This increases the prior odds. It's also more likely to falsely enter into your mind than a random game. This decreases the Bayes factor. But these two effects have the same origin, and their magnitudes are therefore comparable. The degree to which a game is likely to be replicated is also the degree to which it may falsely enter into your mind. The net effect is that the final, posterior odds of the game being truthfully recorded doesn't change as much as you'd think. If you handed me the above game record and claimed that it was an actual, recent game between two people, I may lean towards believing it was real. I may say "huh, it looks like these guys replicated the Immortal Game in their match", rather than "You're lying. You expect me to believe that their random play just happened to exactly replicate the Immortal Game?"
This explains the large swings in the Bayes factor of a human testimony depending on the circumstances, and why it depends so much on the prior odds of the event in question. If the event is intrinsically unlikely, it has low prior odds, but it's also unlikely to enter into your head in the first place, so the Bayes factor correspondingly increases. Conversely, if the event is intrinsically more likely, the Bayes factor decreases.
So human testimony has this somewhat strange property, in that it may "stretch" to cover a great range of priors, even down to numbers like 1e-120. In this way, human testimony is especially efficient at covering low priors. The less likely the prior, the more the Bayes factor of the testimony stretches, so that the final, posterior odds is not as affected as you'd think.
The maximally unlikely, worst case scenario: when the testimony can't stretch more
Now given all this, what kind of claim would be the least likely to be true? You can't just have low prior odds - that only causes the Bayes factor to "stretch" as detailed above. To get around this, we need to consider a claim that's not merely unlikely, but also interesting or remarkable to the human mind in some way. We thus limit the "stretching" of the testimony about the claim, because there is now a special, alternative way for the claimed event to enter your mind. We still want to have low prior odds for the claim, of course: the goal is to maximize the difference between the prior odds, and the likelihood of the idea entering your head.
So the claimed event should be intrinsically very unlikely, but also "special" in some way. In the chess game example, we achieve this by claiming that completely random play by both players resulted in the replication of the Immortal Game. A particular random game is unlikely, and playing the Immortal Game is special. Similarly, one can claim to have won the jackpot in the lottery. A particular set of numbers is unlikely, and winning the jackpot is special. This is how we get minimal posterior odds. This is how we achieve maximum skepticism.
In such examples, as the priors for the claims become increasingly unlikely, the Bayes factor initially stretches commensurately, and the posterior odds remain steady. But then we reach the "stretching limit" of the claimant's testimony, and the posterior decreases quite suddenly. For a lottery, as the claimed winning amount increase from ten dollars to ten thousand to ten million to ten billion, your respective reactions start off like "okay" ($10) and "nice" ($10K), then "I don't know if I believe you" ($10M) - at which you've reach the limit - to suddenly saying "impossible - no way" ($10B).
Here are some more examples of maximally unlikely claims, where you would have maximal cause for skepticism: You can claim that each member of your family shares birthdays with each respective member of your friend's family. A particular set of birthdays is unlikely, and the matching condition is special. You can claim to have been struck by lighting multiple times. Lightning strikes on humans are rare, and personally experiencing such danger is special. You can claim to have been dealt multiple pocket aces in poker. A particular set of hands is rare, and getting the best hand multiple times is special.
You'll recognize the above examples as the ones we studied earlier, from which we obtained the value of 1e8 as the Bayes factor of a human testimony. In other words, that 1e8 value was calculated precisely for these maximally unlikely scenarios, where someone makes an extraordinary claim about an unlikely but special event. It is under these conditions that the resurrection was found to be highly likely.
The maximally unlikely scenario: an example
Again, note the procedure used in calculating our Bayes factor of 1e8: we consider a special claim, then make it more and more outlandish until you can no longer consider it likely. We then measure the Bayes factor at that point. This is why we considered incrementally increasing numbers of shared birthdays and lightning strikes. This is how we get the Bayes Factor that applies to the maximally unlikely scenarios.
Let us walk through the "shared birthdays" problem as an example. Many numbers below are just guesses, but it's the concepts here that are important. We will have plenty of additional examples later with empirically sourced numbers.
Say you write down the list of birthdays for everyone in your family, and your friend happens to come across it. He then earnestly claims that you share the same birthday with him. Now, is this the scenario we want? No: it isn't the maximally unlikely scenario. We have not yet reached the "stretching limit" of the Bayes factor. The prior is still quite large - you have about a 3e-3 chance of sharing your birthday with your friend a priori.
Now, you might think to apply our previously calculated Bayes factor of 1e8 to our friend's claim. If you do so, then we get a posterior odds of about 3e5 - meaning, the claim of shared birthdays would be virtually always true. This is an absurd conclusion.
What went wrong? Well, our Bayes factor of 1e8 was not calculated for this scenario, and it's too large to be used here. The true Bayes factor in this scenario is probably something like 3e3, giving a posterior odd of about 1e1 - about a 90% chance of you two actually sharing birthdays.
Oh no! So the true Bayes factor is only 3e3? Isn't that much smaller than 1e8? Doesn't that ruin the case for Jesus's resurrection? Not at all, because you can't mix and match the priors and Bayes factors from the different scenarios like that. Remember, the prior in this "shared birthdays" scenario is more than 8 orders of magnitude larger compared to the resurrection: 3e-3 versus 1e-11. If you want to use this scenario and its Bayes factor of 3e3, you must also use the prior odds of 3e-3.
Of course, the net effect of doing so is that after applying a single testimony, the posterior odds here is GREATER than they are for the resurrection. In effect, if someone were to argue for using 3e3 as the appropriate Bayes factor for Jesus's resurrection, they'd essentially be arguing that the resurrection was initially quite likely, and so the final result would be even more favorable towards the resurrection.
What if you and your friend's families shared two, three, or four pairs of birthdays? The patterns that we already mentioned applies, with the initial "stretching" of the Bayes factor and the posterior suddenly dropping off after the "stretching limit" is reached. All these scenarios are summarized in the following table:
There are several important things to note:
As we said, human testimony is "stretchy". The Bayes factor will initially stretch to cover increasingly smaller priors, as we make the scenarios incrementally less likely. So the posterior odds are not much affected. In this way, human testimonies are exceptionally good at covering low priors.
This means that the Bayes factor for a human testimony can be smaller than 1e8, but generally only in cases when the prior is large enough to more than make up for it. So trying to argue against a human testimony by assigning it a small Bayes factor in this way is counterproductive.
The "stretching" could continue almost indefinitely - up to Bayes factors like 1e120 and more - if not for the fact that our claim is "special" - It has an alternate way into the human mind because it's interesting or remarkable in some way. This limits the stretching at some point. The "4 pairs" scenario in the above table illustrates this, where the Bayes factor has reached this limit and the posterior odds drop off quickly.
The appropriate, maximally unlikely claims that best correspond to Jesus's resurrection are those "special" claims, which additionally have a tiny prior and therefore a huge Bayes factor. With such claims, where the Bayes factor has been stretched to its limits, we know that its value must be at least as large as any of the earlier, pre-stretch-limited Bayes factors.
Therefore, in such a claim, any Bayes factors we calculate for any specific, empirical example is going to be an UNDERESTIMATE for the testimonies concerning Jesus's resurrection. This lower bound for the maximally skeptical case is what we earlier calculated to be about 1e8.
So there is no escaping that value: the relevant Bayes factor is really about 1e8, and it's fully applicable to the testimonies concerning Jesus's resurrection.
Pulling it all together: the resurrection story revisited
We now have all necessary components to understand a scenario involving multiple pieces of evidence.
Let's say that someone testifies to a rather unlikely event - say, Peter testifies that "Christ is risen". That testimony has a Bayes factor of 1e8, against a prior of 1e-11. That brings the posterior odds to 1e-3. You should not yet assent to Peter's claim.
So, being skeptical, you turn to John, who is Peter's friend and compatriot. You ask him, "hey, is Peter telling the truth?" and he answers "yes". Now, because John's testimony here is not independent of Peter's, it should not get the full Bayes factor of 1e8. Something like 1e2 is more appropriate. That brings the posterior to 1e-1 - still not quite enough for you to assent to the resurrection.
But while you're considering Peter and John's testimonies, Paul - nearly the last person you'd expect to agree with the other two - randomly bursts into the room and says, "Hey guys! Christ is risen!" What is the Bayes factor for that testimony? Because of the large degree of independence, Paul's testimony should get a large portion of the full 1e8 - easily overpowering the remaining 1e-1 odds, and fully shifting the posterior odds to be much greater than 1.
Paul's testimony, with full dependence factor
Do you doubt that Paul's testimony is enough? Then consider the following: Taking the full dependence factor into account, the Bayes' factor of Paul's testimony is, by definition, given by the following:
P(Paul|John, Peter, Resurrection) / P(Paul|John, Peter, ~Resurrection)
Where "Paul", "John", and "Peter" stand for each of their respective testimonies, and "Resurrection" or "~Resurrection" is our hypothesis in question, whether the resurrection happened or not.
Now, as ever, let us approach this empirically. P(Paul|John, Peter, Resurrection) is not all that unlikely. This is the probability of an opponent of Christianity giving a miraculous conversion testimony. Even apart from Apostle Paul himself, stories like this are old hat. You can't be a Christian for very long without tripping across a load of them.
Then what about P(Paul|John, Peter, ~Resurrection)? This is like the probability of a Paul-like miraculous conversion to your opponent's religion, DESPITE the fact that the religion is false. To get at this number, we only need to pick a religion that both you and I agree is false. Islam or Hinduism will do nicely, as they're mutually exclusive world religions: everyone can pick at least one of those as their "false" example. So, how many Paul-like miraculous conversion stories are there to that religion?
I have not heard of a single case. But it's not just me - I don't think even GOOGLE has heard of a single case. Google search will return different results for different people at different places and time, but my experiences on this front are still telling.
When I searched for "conversion stories to Islam", I got many cases of exactly what I searched for - conversion stories to Islam. So it's not as if Google has some anti-Muslim or pro-western agenda which prevents them from showing Islam-positive search results, nor is there a shortage of conversion stories to Islam on the internet. This is not surprising - the internet is a big place and Google is good at what it does.
But, when I searched for "miraculous conversion stories to Islam", the majority of the results, including the top result, was for Muslims converting TO CHRISTIANITY. And of the few results which actually described conversions to Islam, I could not find one which actually claimed to be miraculous in nature. Most of them are only of the "Islam made sense after I studied it" type. And none of them involved anyone who was as rabidly anti-Islam as Paul was anti-Christian.
Do you understand how remarkable this is? Even Google couldn't find me a single example of a miraculous, Paul-like conversion story to Islam, and when asked to do so it actually returned mostly conversion stories FROM Islam TO Christianity, despite "Christianity" not being in the query at all. That should give you an idea for the relative prevalence of such stories. It's reflective of the absolute dominance that P(Paul|John, Peter, Resurrection) has over P(Paul|John, Peter, ~Resurrection).
In fact, from this experiment, we can see that the magnitude of this dominance - that is, the Bayes factor of Paul's testimony - is in the same ballpark as the Bayes factor of a Google search itself, which is worth many orders of magnitude. It easily and greatly outpaces the numbers like 1e1.
Searching for "miraculous conversion stories to Hinduism" gave me mostly similar results. Nearly the entire first page is about Hindus converting to Christianity.
So, here is the challenge: do you believe that Paul's testimony is not enough? That it can't cover the remaining 1e-1 odds? Then you need to be able to back that up empirically. You need to give me one instance of a miraculous conversion to Hinduism or Islam by a former opponent, for every 10 instances of a miraculous conversion to Christianity that I could cite. Good luck with that, given that even explicit Google searches for such conversion stories return far more cases supporting the Christian position.
Back to the resurrection story
So, after hearing Paul's testimony, and given its large degree of independence, you assign it a Bayes factor fairly close to the full 1e8 value. This easily overcomes the remaining prior, and pushes the posterior odds firmly to favor the resurrection. You should now firmly believe that Jesus did rise from the dead.
And as if that wasn't enough, you then encounter a flood of people all claiming that Jesus rose from the dead - the remaining members of the twelve apostles and other disciples, James, and a crowd of more than 500 people, just to name the remaining witnesses in 1 Corinthians 15. After considering all of their testimony, their claim is now beyond the shadow of any doubt: Jesus Christ almost certainly rose from the dead.
Human testimonies stretch to cover the rest of the Bible
Ah - but what about the other miracles in Christianity? Sure, the resurrection might be well-attested, but what about the numerous other miracles in the Bible which has barely any evidence behind it? For example, only Matthew mentions the resurrection of other people at the time of Jesus's death. He only mentions it briefly, in passing. Many of the remarkable miracles during the Exodus are also mentioned only in that book. The Bayes factor of a single testimony can't possibly cover all of these other stories. How could a Christian believe in such things, if such evidence is inadequate according to our methodology?
So, what have we achieved in this deeper dive into human testimonies?
We've seen that, while there is in fact high variability in the strength of a human testimony, our value of 1e8 for their Bayes factor was already calculated for the maximally pro-skeptical scenario - where the most remarkable, noteworthy claim is being made about a highly unlikely event. This was most fitting scenario for the resurrection testimonies, which gave the lowest posterior odds. And yet, even under these conditions the resurrection proved to be overwhelmingly likely.
Along the way, we've explained why this 1e8 might mistakenly feel too large, when you ignore the priors that the human testimonies have to overcome. For instance, a human testimony can have a smaller Bayes factor like 1e2 - if it's about an event which is already quite probable, like a coin flip or a yes/no question. Conversely, since the resurrection is a highly improbable event, testimonies concerning it should be given a higher value than in our other examples.
This relates to how human testimonies may "stretch" to cover smaller priors. If there is no special way for a particular falsehood to enter into your mind, this stretching can extend to absolutely minuscule priors (as in the record of a chess game). Incidentally, this gave us a nice bonus, in that it justifies our belief in the other miracles in the Bible aside from the resurrection. Yes, these miracles have low priors on their own. But once we accept Jesus, the testimonies about them can easily "stretch" to cover their priors, as such miracles cease to be the most remarkable, special thing that can happen in a world where Jesus rose from the dead.
Putting all this together, we repeated our earlier calculation for the odds of the resurrection, this time taking the dependence factors fully into account. We saw that the strength of just Peter and Paul's testimonies, even with full dependence factors, was easily enough to put the odds firmly in the "likely" side. The rest of the testimonies in 1 Corinthians 15 then puts the resurrection beyond any reasonable doubt.
So, we now have a good idea of how human testimonies comes together. We understand its anatomy and its behavior. And this deeper dive into human testimonies made sense of our intuitions, verified our earlier thinking, and validated our previous conclusion.
Double checking the Bayes factor of a human testimony
Everything above points to 1e8 as the appropriate Bayes factor for the kind of testimonies given for Jesus's resurrection. But for some time now, I've been promising additional examples that would provide more empirical backing for this number. Let us get to those now.
The reporting of experimental results
Some people simply cites "science" against anything outside their narrow, naturalistic worldview. But have you wondered how science actually gets done in the real world?
In a typical hypothesis-testing scenario, a Bayes factor of 1e1 is considered a decent amount of evidence, and 1e2 is considered very strong. Conversely, negative logarithmic values are considered evidence against the hypothesis. Depending on the the specific field of science, the results can often be far stronger than these typical values.
Now, we know that human testimony must be much more powerful still than the reports containing such results. Otherwise, how could you trust these reports? If the human had larger uncertainties than the results, a human report of such results would be worthless. The fact that you generally believe such reports means that you already believe that the human testimony is much stronger.
Of course, not every experimental report can be trusted. They should be replicated whenever possible, and they can be sometimes overturned. But no scientist ever replicates every experiment. They instead generally trust the testimony of others. To require otherwise would make it impossible to do science. This is how the vast majority of a scientist's expertise is built up, and it indicates that the Bayes factor of a human testimony is vastly greater than 1e1 or 1e2.
The frequency of lies
How often have you been lied to? This is perhaps the go-to questions for people who disbelieve the 1e8 value. In doing so they tend to make a set of common mistakes.
Some may say, "people lie way more than 1 out of a hundred million (1e8) times! There's no way that human honesty has odds of 1e8!" But this makes the mistake of confusing a Bayes factor with the posterior odds. They're also forgetting that the bulk of the Bayes factor comes from the idea entering your head in the first place, and is quite independent of human honesty.
One calculation starts like this: let's say that people have about 10 opportunities to nontrivially lie to you in a given day. Multiplying by about 300 days a year and assuming that you're about 30 years of age, this amounts to about 100,000 (1e5) opportunities in your life for someone to tell you a nontrivial lie.
At this point, many make the mistake of dividing 1e5 by 1e8, and conclude that a Bayes' factor of 1e8 would imply a 1e-3 odds of you having been lied to in your lifetime - an obviously absurd conclusion. This mistake comes from confusing the Bayes factor with the posterior odds.
The correct math here requires getting the prior and posterior odds, and getting the ratio between them. In essence, we're using the second of the two ways to calculate a Bayes factor: to measure it by how much it moves the odds, from the prior to the posterior.
So, how often have you been nontrivially lied to, in your 30 years of life? Let's say 1,000 (1e3) times. That corresponds to roughly 3 nontrivial lies per month. That means that the posterior odds of a lie is 1e3 out of 1e5 opportunities, or 1e-2. The posterior odds of a truth-telling is therefore 1e2. That is, people generally turn out to have lied about 1% of the time.
But what are the prior odds? Remember, we're specifically interested in someone making a positive assertion about something that happened - such as "I got into a car accident", "I went to Harvard", or "I was vacationing in France that day". In such cases, the priors are quite small. Most specific events are improbable. Let us generously assign 1e-3 as the prior odds of the statement being true.
Then, the Bayes factor is the factor which turns that 1e-3 to the posterior odds of 1e2. In this case, it's 1e5, because 1e-3 * 1e5 = 1e2.
Here, people often make another mistake: they say, "aha! 1e5 is still smaller than 1e8!" But they're forgetting that a prior odds of 1e-3 is still nowhere enough to stretch the Bayes factor to its limit. Remember, human testimony is exceptionally good at overcoming low priors. Compared to the typical lies mentioned above, the claims we're discussing involve events like winning the lottery, being struck by lightning, or someone rising from the dead. Such events will have far smaller priors, and therefore far larger Bayes factors. As I mentioned before: this is why any specific Bayes factors we calculate for any empirical example is going to be an UNDERESTIMATE for the testimonies concerning Jesus's resurrection. The larger the prior odds are in the example, the more of an underestimate the calculated Bayes factor will be.
In addition, the kind testimonies involved in Jesus's resurrection are not trite, everyday lies. We're specifically concerned about sincere, insistent, enduring, and life-changing personal testimonies. This set of conditions easily adds a couple of orders of magnitude to the Bayes factor.
It's also important to note here that we're looking for lies, not mistakes. People makes mistakes all the time - far more frequently than they lie. So we are not talking about the various opinions people have about relationships or medicine or politics. Rather, we are concerned with people telling stories about something that personally, directly happened to them.
So, pulling the above together, we see that 1e5 is a very weak lower bound on the strength of a human testimony: a typical lie has large priors and is generally not very serious, which both lower the Bayes factor. So for a testimony about an event like the resurrection, 1e8 is quite appropriate.
Car accidents
Imagine that you've arranged to have an important meeting with me on a particular date, but then I fail to show up. You're understandably peeved, but I call you soon afterwards saying, "I got into a car accident. I'm okay. But I'm really sorry that I couldn't make it to our meeting today. Can we reschedule?"
Now, would you believe my story? Did I really get into a car accident on the day of our appointment? What would you assign as the probability that I'm telling the truth?
The average driver gets into a car accident roughly once in 18 years. That's about once every 6500 days. So the prior odds for getting into a car accident on a particular day is 1/6500. If you choose to believe me - say, you think there's more than a 90% chance that I really was in an accident - then you've changed the odds for my car accident from 1/6500 to 10/1, and you've therefore granted my phone call a Bayes factor of 65000 - or nearly 1e5.
From our earlier calculation, a Bayes factor of 1e5 would already be sufficient to make Jesus's resurrection quite likely. Peter and Paul's independent testimonies would add up to 1e10, and the great mass of testimonies by everyone else - James, the other disciples and apostles, and the crowd of 500 - would easily contribute at least a factor of 1e1. That's amply sufficient to overcome the initial 1e-11 prior.
In other words, if you would believe that I got into a car accident, you ought also to believe in the resurrection. Otherwise you're being inconsistent. If you wish to disbelieve the resurrection, you must also be the kind of person who says, "I don't believe you. I think you're lying about the car accident. You need to give me additional evidence before I believe that something that unlikely happened".
Ah, but maybe the people who are skeptical of the car accident are right? Maybe we should be more skeptical in general? It might be the polite thing to do to believe someone in such situations, but how do we know that that's actually the mathematically right thing to do?
Well, this is where the fact that this actually happened to me comes into play. I once got into a car accident on my way to a wedding. I was not hurt, nor was my car seriously damaged - but the whole affair did cause me to miss the entire wedding ceremony. I only managed to show up for the reception afterwards. That day, I told numerous people that I had gotten into a car accident, and gave it as my excuse for missing the ceremony. Not a single one of these people doubted me in the slightest: they all believed me. And they were right to do so, because I had in fact gotten into a car accident.
So if the trust of the other wedding guests have any weight at all, the posterior odds here should exceed 1e1 by a good amount. So 1e5 is the right Bayes factor here, at an absolute minimum. Of course, this is the same number as in "the frequency of lies" example, which makes sense since a car accident is something you may possibly lie about. As in that example, this is only a lower bound for the right Bayes factor, as the prior odds are quite large.
Now, what if someone claims to have gotten into two car accidents in one day? Assuming independence, the odds of such an event is 2e-8. There is some dependence factors here, but it's not too bad. If there were a significantly increased chance of a second accident in the same day, you would not be allowed to drive after the first. In fact, you may become more cautious after one accident, making the second one less likely. But let's be conservative here, and say that the net odds including dependence is 1e-7.
Now, if you don't believe that human testimonies can "stretch" - if you think that 1e5 is the limit - then anyone claiming to have been in two car accidents in one day must be basically lying. With these numbers, the posterior odds would be only 1e-2. So such an outlandish event must be simply too unlikely to be believed, on a single human testimony.
Do you like Taylor Swift? Because you just called her a liar. On a TV show, she claimed to have been in two car accidents in one of the most important days of her career. And if you think her own testimony can't cover the low prior odds, then you must be quite certain that she lied. Of course, your judgement would go against the reactions of everyone on the show, who all seem to take her at her word. It would also go against the judgement of the media outlets that related her story without question. You would need to somehow convince yourself that you and you alone have a unique insight into Taylor Swift and her lies.
Again, if the unanimous trust of all who heard her story is to have any weight at all, the posterior odds here should be, at the very least, 1e1. This gives her testimony a Bayes factor of at least 1e8. And this is based on a very flimsy testimony: I mean, I don't think Taylor Swift is a liar, but I don't know her to be especially honest, either. She's trying to be funny and entertaining during a TV show. The whole story only takes a couple of minutes to tell. And even with such inadequacies, her testimony has a Bayes factor of 1e8 or more. The testimonies about Jesus's resurrection must have a greater Bayes factor still.
But maybe you're still clinging to the idea that Taylor lied. Maybe I was a fool to believe her story. Maybe everyone on that show are all fools also. How could we know for sure? Well, here's some independent verification. Note that I found this article only after I decided to believe her story, and the people on the TV show are clearly hearing her story for the first time. So everyone had already decided to give her a Bayes factor of 1e8, just on her testimony - and the independent verification validates the trust they placed in her story, and therefore also that Bayes factor.
Human death
You're talking to a friend that you haven't seen in a year, and you're exchanging news about mutual acquaintances. You ask, "how's Emma doing?" Your friend then replies and says:
"Oh, you haven't heard? Emma... is dead. She was killed in a car accident. And you know how she was really close to her mom? Well, when her mom heard the news of Emma's death, she committed suicide - they say that they had the funeral ceremony for both of them together."
You may have guessed that this, too, actually happened to me. A friend of mine told me this tragic story about a girl we both knew. Don't be too concerned - the name of the girl has been changed, and this happened long ago - long enough ago that all the parties involved must have gotten well past the shock and the grief.
But, let us turn back to the question at hand. Should I trust my friend, on this very unlikely story? The yearly car accident fatality rate is about 1 per 10,000. The suicide rate is about the same. My friend's story, therefore, has an independent prior odds of about 1e-8 of being true. There is some dependence factors which increase the odds (a mother is more likely to commit suicide after her daughter's death), but the specifics of the story (the specific cause and timing of the suicide) would again decrease the odds. Let's be conservative again and say that the prior odds is about 1e-7.
I'll go ahead and tell you that I did believe my friend. I did not really doubt his story. If I had to put down a number for my degree of belief, I would say that I gave his story about a 1e2 odds of being true. So the odds for this sequence of events went from a prior of 1e-7 to a posterior of 1e2, and therefore the Bayes factor for my friend's testimony is about 1e9.
But was I right to trust my friend? Maybe I should have said back to him, "I don't believe you. Your story is just too ludicrous"? Well, as it turns out, I did get independent verification for a good chunk of this story later on. I really was right to trust my friend. Given that this is only a single instance of verification, this only validates that I was right to trust my friend, but not necessarily that I was correct to give the story a posterior odds of 1e2. So, at a minimum, I was definitely justified in giving my friend at least 1e7 for the Bayes factor as a lower bound, and I feel that the correct value should actually be closer to 1e9.
LinkedIn claim
Some of the previous examples were drawn from stories and experiences that I have personally lived through and verified. But perhaps you're not convinced by the stories from my past. Fair enough - they're event that I have directly experienced, so they're empirical for me, but they're not empirical for you.
Here, then, is a calculation that anyone on the internet can verify to get an empirical value for the Bayes factor of a human testimony. All of the raw numbers in the following calculation are provided for the time of this writing (June 2016).
Go on LinkedIn, and search for "PhD physics Harvard". You'll find many people who claim to be in the PhD program at Harvard University. You may need to upgrade your LinkedIn account to see the profiles for these people, if they're outside your network. Now, are these people telling the truth? And what ought we make of their claim that they're getting the most advanced degree in the most challenging field from the most prestigious university in the world? And what is the Bayes factor for that claim?
To address this, we first need to find the prior odds for someone on LinkedIn being in the Harvard physics PhD program. For this, we'll need to gather up some numbers - all of which are readily available online.
First, let's get the number of people in Harvard's physics PhD program. This is easy enough - their department's webpage tells you that they have about 200 graduate students.
It's also easy to find the number of people on LinkedIn. Their website will tell you that they have more than 128 million registered members in the United States.
Now, we'll make the generous assumption that all 200 people in Harvard's physics PhD program are on LinkedIn. This means that the prior odds for someone on LinkedIn actually being in the program is about 200/128 million, or about 1e-6.
What about the posterior odds? Well, we can take the people on LinkedIn who claim to be in the Harvard physics PhD program, and actually investigate them one by one. Many research groups have their rosters published online, so you can easily find out whether someone really is in a physics research group at Harvard. You may also find their scientific publications or teaching records online, all of which can confirm their status in the program.
So, I searched on LinkedIn for "PhD physics Harvard". I spot checked more than a dozen people from the search results who claimed to be in the Harvard physics PhD program. I chose my sample over many pages across the unfiltered LinkedIn search results, so that the "relevance" of the search results to me will not influence my sampling.
What was the result? I found that every single person I checked was telling the truth. I could verify each of their claim independently from the LinkedIn page, nearly always from an official Harvard physics department page. Since I had checked over a dozen people, this represents a posterior odds of 1e1 at a minimum for these people really being in the Harvard physics PhD program.
This means that, at a minimum, the mere claim of these individuals on LinkedIn changed the odds for that claim, from a prior value of 1e-6 to a posterior value of 1e1. Therefore, the Bayes factor for these claims have about 1e7 as a lower bound. The actual value is therefore well within range of the 1e8 value that we've been using.
It's also important to note how weak a claim on LinkedIn is compared to the kind of earnest, personal testimony that we're interested in. Anyone can get a LinkedIn account; they just have to sign up for it. They can then say whatever they want in that account. Furthermore, there is not much concrete negative consequences for lying, while the incentive of getting a job or a business contact can be quite appealing. At worst you'd lose a job that you'd have not gotten otherwise anyway. But even with all this going against it, the people on LinkedIn turn out to be quite trustworthy, with the Bayes factor for their claims having a value near 1e8.
The Bayes factor for the disciples testifying to Christ's resurrection must be worth at least that much.
Fake 9/11 victims
Here is yet another example from which we can empirically derive the Bayes factor for a human testimony.
The September 11 terrorist attacks killed about 3000 people. It is the worst terrorist attack in world history to date. As such, it caused a great deal of shared grief and an outpouring of sympathy for the survivors and the families of its victims.
Of course, human being being what they are, some people falsely claimed that a close loved one had died in the attacks. This got them a lot of sympathy - and more importantly, it got them a great deal of aid money, exceeding a hundred of thousand of dollars in some cases.
This naturally leads us to ask - how reliable was a person's claim that they had lost a loved one in the 9/11 attacks? What was the Bayes factor for such a claim? The numbers for this calculation are readily available. We just have to assemble them.
First, let's calculate the prior probability that someone really did lose a close loved one in the 9-11 attacks. We will assume that every one of the 3000 victims had about 4 loved ones (father, mother, sister, son, etc) whom we can consider "close", and that all of these loved ones lived in New York City. This gives 12,000, or about 1e4, close relation of the victims in a city with a population of 1e7. Therefore, the prior odds for a random person in New York City actually having a close loved one as a victim is about 1e-3.
Now, if someone claims that they had a close loved one die, what is the posterior odds that this person is actually telling the truth? One may assume that a vast majority of the 1e4 actual close relations of the victims made that claim. But how many false claims were mixed in with those? The specific number is not possible to determine (as someone could have lied so well that they were never suspected), but the article I previously linked mentions numbers like "dozens", "two dozen", or "37 arrests". Taking these numbers into account, let us be generous here and assume that there were 100, or 1e2, false claimants. The posterior odds are therefore 1e4:1e2, which equals 1e2.
Therefore, the Bayes factor for someone claiming to have lost a loved one in the September 11th terrorist attacks is sufficient to take the odds from an empirically calculated prior value of 1e-3 to an empirically calculated posterior value of 1e2 - so it must be given a value of 1e5.
Nearly all of the numbers here are from Wikipedia or the New York Times. You can follow up on their sources and verify the values yourself. In the few places where I had to make assumptions, they have a definitive bias towards reducing the Bayes factor - for example, the people who lost loved ones are not all confined to New York City, and 100 false claimants are a good deal more than two dozen. There's probably also a greater tendency for the truth-tellers to communicate their loss to more people in cases like these. Therefore, 1e5 is an underestimate of the true Bayes factor. The actual value is greater - 1e6 seems like a reasonable guess.
Consider what this means: even when there was a clear reason to lie - that is, even when there was cold, hard cash at stake as a tangible reward for lying - people turned out to be fairly reliable overall. The Bayes factor for their earnest claim about the personal tragedy of losing a loved one turned out to be about 1e6.
Now, the types of testimonies we're interested in would not have the explicit possibility of fraud as a precondition. It would also have a much lower prior, which again would stretch the Bayes factor much further: remember that human testimony is exceptionally efficient at overcoming lower priors. Therefore a value of 1e8 for the kind of claims we care about is quite appropriate.
(jackson pollck painting fraud)
(claimants to be Grand Duchess Anastasia)
One in a million events happen every month
This phenomenon goes by the name of "Littlewood's law": we start by assuming that a person witnesses an "event" every second. There are about 3 million seconds in a month, and humans are alert for roughly 1/3 of those seconds, resulting in a typical person witnessing about a million events per month. So then, it's expected that one of these events will have a prior probability of one in a million.
This has been used against the idea of the miracles - and certainly, if you have the rather simplistic view where you define a "miracle" as "an unlikely event", Littlewood's law would show that such "miracles" are not exceptional.
However, that misses a more important point, that reports of such event are often reliable. One need not be an outstandingly honest individual to make an "one-in-a-million" claim. One simply needs to report the most unlikely, exceptional thing that happened to them in the last month - which people do rather regularly. Even if you make a large concession and say that half of such reports are lies, that means this event's prior odds of 1e-6 turned into a posterior odds of 1e0, giving 1e6 as the Bayes factor for such a report.
In fact, applying the raw form of Littlewood's law to the resurrection testimonies actually gives a Bayes factor in excess of 1e8. For the disciples maintained their testimonies not for a month, but for their whole lives - a period lasting decades. Theirs was a claim about the most exceptional thing they had witnessed in that long period. Using the same argument as above, the most exceptional event that happened in the last 30 years is 360 times less likely than the corresponding event in a month, because that's how many months are in 30 years. Therefore, a report of such an event would have a Bayes factor of 3.6e8, even if you make the rather large concession that half of such reports are lies.
Perhaps a more reasonable set of assumptions would be that a report of a resurrection would need a minute's worth of events to be actually observed, rather than a second. This would correspond to a length of a short conversation, or an extended greeting. This means that "events" of this type last a minute rather than a second, which reduces the Bayes factor by 60. But reports about the most exceptional minute over the course of 30 years probably has better than even odds of being true - a posterior odds 1e1 seems appropriate. Making these adjustments, the Bayes factor turns out to be 0.6e8.
But at this point we're discussing minutiae. In the end, a personal claim which endures for 30 years has a Bayes factor of around 1e8. We can then add the "sincere, insistent, and life-changing" conditions on top of that, and that makes 1e8 a good, safe value to use as the Bayes factor for the type of testimony in Jesus's resurrection reports.
Video of a lottery winner
As one more confirmation of that 1e8 number, take a look at this video - it shows a woman's reaction to an acquaintance who claims to have won the lottery. Now, does that woman seem like a gullible idiot to you? I don't feel that way. She starts off quite skeptical, but not dismissively so. Then you can see the man's sincerity working on her - her degree of belief is clearly somewhere around even odds right before the numbers are confirmed. I think her overall reaction is pretty rational.
Now, there are some small differences between the video and the previous examples. For instance, she already knows that there's a winner out there, which increases the prior odds. But on the other hand, the woman's belief is achieved with little effort on the man's part, taking only a few minutes of insistence. The man being her acquaintance, and the fact that he comes up to her during the filming of this video, also increases the chances for something like a practical joke - which is an additional factor that his personal claim has to overcome.
On the whole, you can see her mind being pulled through a Bayes factor of something like 1e6 within mere minutes, in good accord with rationality, in a situation pretty similar to what we described in the previous examples. So 1e8 for something like the disciple's testimony about the resurrection is quite reasonable.
Summary of the findings
These are the ways we've calculated the Bayes factor of a human testimony. Remember, all of these are UNDERESTIMATES of the Bayes factor for the testimonies for Jesus's resurrection.
|
Estimation method
|
Bayes factor
|
Notes
|
|
3 shared birthdays
|
1e7.5
|
|
|
lottery winner
|
1e8
|
|
|
2 royal flushes
|
1e9
|
|
|
5 pocket aces
|
1e7.5
|
|
|
quadruplets/quintuplets
|
1e7
|
|
|
2 lightning strikes
|
1e9.5
|
|
|
report of experiments
|
>> 1e2
|
vast underestimate
|
|
frequency of lies
|
> 1e5
|
lower BF due to large prior
|
|
car accident
|
> 1e5
|
lower BF due to large prior
|
|
2 car accidents in a day
|
1e8
|
|
|
human death
|
1e7 to 1e9
|
a friend’s testimony
|
|
LinkedIn claim
|
> 1e7
|
|
|
fake 9/11 victims
|
> 1e6
|
lower BF due to large prior, clear reason to lie
|
|
Littlewood’s law
|
1e8
|
|
|
lottery winner video
|
1e6
|
happens in a few minutes
|
|
historical comparisons
|
> 1e9
|
covered in a later chapter
|
We began by examining our gut feelings on how much credit we would give to someone who made extraordinary claims, like having won the lottery or been struck by lightning. From this initial calculation, using just some intuition, we got a variety of numbers for the Bayes factor of a human testimony, ranging around 1e7 to 1e9. The number we ended up using, 1e8, started from these calculations.
That's a good start, but we wanted empirical backing. The first natural experiment we used to verify this number was the case of the people who lied about winning the 1.6 billion dollar Powerball lottery. The result from this calculation was about as good as it could possibly be expected; 1e8 really turned out to be the correct order of magnitude for the Bayes factor, when someone claimed that they had they had won the lottery.
We also considered the fact that human testimony must be vastly more powerful than the results of a typical experiment, which have Bayes factors around 1e2. Otherwise, you could not trust the report of experimental results, and science would grind to a halt.
We then considered how often people lie to us. We found that even weak, off-hand statements making rather unremarkable claims often have a Bayes factor exceeding 1e5. Adding the "sincere, insistent, and enduring" condition on top of that, plus accounting for the "stretchiness" of human testimony, could easily bring this to around 1e8.
We then investigated the case of someone missing an appointment due to a car accident. The claim of a car accident on a specific day turned out to have a Bayes factor of 1e5 as a lower bound. The claim of two car accidents in a single day had a Bayes factor of 1e8. This again illustrates how human testimony "stretches" to meet a lower prior.
We next investigated the tragic story of a young woman dying in a car accident, and her mother committing suicide when she heard the news. The testimony of the person who related this story was calculated to have a Bayes factor of 1e7 as a lower bound, while its true value was estimated to be around 1e9.
For the claims of being in Harvard's physics PhD program, the Bayes factor was found to have a lower bound of 1e7 - of course, the most likely value would be higher. And for the case of people claiming to have lost a close loved one in the 9/11 attacks, the Bayes factor turned out to be about 1e6, despite the fact that there was cold, hard cash to be won as a strong temptation to lie.
Furthermore, we saw that making a claim with a Bayes factor of 1e8 doesn't require some extraordinary honesty or accuracy. Since Littlewood's law says that one in a million events happen every month, and one in 1e8 events around every decade, merely reporting such events with mediocre accuracy gives you a Bayes factor of 1e6 or 1e8 respectively, even if such reports are wrong half the time.
Lastly, we checked this value on a gut level. We saw a video of a woman whose degree of belief changed by around 1e6, in a matter of minutes, by a man who claimed to have won the lottery. In the video, she was clearly rational and displayed the appropriate amount of skepticism, but in the end her decision to give the lottery winner the benefit of doubt turned out to be the correct one.
And here's one more double check, which we'll cover fully a few chapters later: consider all the personal testimonies about a resurrection made throughout world history, which pass the "sincere, insistent, enduring, and life-changing" condition. How many such testimonies are there? And what does that imply about the Bayes factor of such a testimony?
As we'll see, there are essentially no non-Christian figures who have had such a resurrection claim about them. There are many claims at the "some people say..." level, but none of them reach the level of a sincere, insistent, enduring, and life-changing personal claims of the kind we're looking for. Given that billions of people have died with no resurrection claims about them, this means that such a resurrection testimony is at least an one-in-a billion (1e9) event - and so it must be accorded a correspondingly large Bayes factor.
The strength of a human testimony is firmly established and understood.
It is important to note that all of these examples were merely the first ones that came to my mind which I could also get good numbers for. There is not a set of other examples which I chose not to use because they didn't suit my purpose. There is no conscious selection bias here. In fact, I encourage you to come up with your own examples through which you can compute the Bayes factor of a human testimony. Compare your answer with mine, and independently verify my values.
It is also important to acknowledge that there is variance in the Bayes factors. By far the largest component is the "stretchiness" of human testimony, which causes claims with higher prior odds to have lower Bayes factors, and vice versa. So for a claim like Jesus's resurrection, 1e8 is a typically a good, conservative value. This is verified through the many examples above with empirical backing.
This can further change slightly when we put additional conditions on it. The relatively higher value of 1e9 was obtained for a friend telling me an unlikely story, and its greater Bayes factor can perhaps be attributed to the credit of that friendship. On the other hand, claims of losing loved ones in the 9/11 attack has a Bayes factor of 1e6, and this lower value can be partially attributed to the explicit possibility of fraud. It seems that such considerations can shift the Bayes factor a little, by an orders of magnitude or so.
But even if you go with the lowball value of 1e6, the evidence for the resurrection is amply sufficient. Just Peter and Paul's independent testimonies would combine for a Bayes factor of 1e12, which overcomes the prior odds of 1e-11. Then the remaining testimonies in 1 Corinthians 15 would drive the posterior odds far beyond any reasonable doubt. Meaning, EVEN IF you KNOW that the disciples had a good reason to be deceptive or delusional, there's STILL enough evidence in their testimonies to conclude that Jesus did really rise from the dead. That's how strong the case for the resurrection is.
Can naturalistic explanations account for the resurrection testimonies?
So, the previous Bayesian analysis compels us to believe that Jesus really rose from the dead. But, as an additional layer of verification, let's approach the problem from a different angle, and see if we come to the same conclusion.
In our analysis, the odds for Jesus's resurrection went from a prior value of 1e-11 to a posterior value far greater than 1 - meaning, the Bayes factor for the testimonies in 1 Corinthians 15 was well in excess of 1e11. That is to say, the evidence of those testimonies is - at the very least - 1e11 times better explained by an actual resurrection than by naturalistic alternatives.
Now, if you want to cling to a naturalistic alternative, you must believe that this Bayes factor value is incorrect. That it is not really that large. That the true value is insufficient to overcome the small prior odds. That a naturalistic alternative can sufficiently explain the evidence, so as to make an actual resurrection unnecessary.
Well, can you demonstrate that empirically?
If naturalism can sufficiently explain the evidence for Jesus's resurrection, I expect there to be some non-resurrection cases where the same level of evidence was achieved through ordinary means - through naturalistic chance, as it were. It would be a strange naturalistic explanation indeed that works only once for the specific case that we're trying to explain, and never works again.
Here's what I mean: let's say that you think the resurrection testimonies are totally worthless and changes nothing about the probability that Jesus rose from the dead. This would correspond to a Bayes factor of 1 (or 1e0), meaning that a non-resurrection is equally likely to produce these testimonies as a genuine resurrection.
As a conservative estimate, let us say that there have been 1e9 reportable, non-Christian, naturalistic deaths throughout world history. Then, a Bayes factor of 1 would correspond to saying that all 1e9 of those people were as likely as Jesus to produce a resurrection story, each as likely as he to produce the level of evidence given in 1 Corinthians 15. Then, roughly speaking, there ought to be a good fraction of a billion comparable cases. Well, where are they? Can you produce these resurrection reports?
Say that you're willing to be slightly more reasonable: you think the Bayes factor for the Jesus's resurrection reports is 1e6 - far smaller than 1e11, but still significantly greater than 1. Effectively, you believe that the testimonies clearly do count as evidence, but that it's just not enough to overcome the prior. Well, a Bayes factor of 1e6 corresponds to saying that a non-resurrection still has one millionth the chance of producing New-Testament level of testimonies compared to a genuine resurrection. Again, with those odds, given that there have been at least 1e9 people whose deaths were reported throughout human history, this means that you should still be able to produce on the order of a thousand accounts of someone rising from the dead, each with about as much evidence as the New Testament has for Jesus's resurrection.
You can easily do the same calculation for a Bayes factor of 1e9. Following the examples above, if you think that the Bayes factor is only that large, then you should still be able to find maybe one other case where a non-Christian, natural death produced a comparable level of evidence as the New Testament has for Jesus's resurrection.
Validating even larger Bayes factors with historical records
Ah, but what if you believe, as I do, that the Bayes factor is far larger? That Peter's testimony by itself already has a Bayes factor of at least 1e8, and that Peter and Paul's testimonies together has a Bayes factor well over 1e11?
Well, Peter's testimony by itself is pretty clear. If we consider it by itself - that is, independently, as if Peter's testimony was the only piece of evidence for Christ's resurrection - then we can simply apply the above logic. So if Peter's Bayes factor really is 1e8, I should be able to find on the order of 10 other resurrection reports throughout history which have a similar level of evidence. If the Bayes factor is actually smaller, I'll be able to find more such reports. If the Bayes factor is greater, then I'll be able to find less.
For Peter and Paul's testimonies together, if the Bayes factor there is really well over 1e11, then I won't be able to find a single resurrection report with enough evidence to match their testimony. In fact, since 1e11 is 100 times larger than 1e9, this would require observing less than one of something. How does that work out?
While we can't observe less than one instance of something, we can observe how close the closest instance comes. Let's work through our numbers: 1e11 is 1e9 raised to the 11/9th power. So, if 1e11 is the Bayes factor for Peter and Paul's testimonies, You'd expect the nearest case of a non-Christian resurrection story to have about 9/11th of the evidence of Peter and Paul's testimonies combined. In other words, it would come pretty close to matching Peter and Paul's combined testimonies. So the closest case may come near to the edge of what may be considered "comparable". For instance, this hypothetical non-Christian resurrection story may perhaps have the evidence of two fully committed personal testimonies, but the two might only be strangers instead of mortal enemies.
If you assume that Peter and Paul's testimonies are almost completely independent, as I have in my calculation at the beginning, their combined testimonies gives a Bayes factor of 1e16. How could we verify that? Again, we look to the historical record. If that 1e16 is correct, then throughout the 1e9 reportable deaths in history we would expect a resurrection report with a maximum evidence reaching 9/16th of the level of Peter and Paul's combined testimonies. 9/16 is a little more than 50%, so that might correspond to one exceptionally well-documented individual testifying to the resurrection. If that is what we find, our value of 1e16 is roughly validated. If we find less than that, that means Peter and Paul's combined testimonies may have an even larger Bayes factor.
Think of the process in this way: say that there's a record of a million coin flips, which is generally considered to be randomly generated. While examining that record, I come across a sequence of 10 heads in a row, and say "Wow, that's amazing! These coin flips couldn't have been random!" Now, if you wanted to debunk me by showing that random chance can easily produce such sequences, you can say "Actually, the chances of getting 10 heads in a row randomly is only 1 / 2^10, or about 1e-3. The Bayes factor of this sequence for your 'non-random' hypothesis is therefore only 1e3. In a million coin flips, you'd expect to see something like this about a thousand times". You can then proceed to point out those thousand other "10-heads-in-a-row" sequences in the coin flip record, and that would validate your Bayes factor estimation.
However, let's say that I then come across a sequence of 60 heads in a row. I say again, "Wow, that's amazing! These coin flips are clearly non-random! I think the chances of a sequence like this is 1 in 1e18". How could I empirically prove that my estimate is correct, when the probability is so small? Wouldn't I naturally expect zero such "60-heads-in-a-row" sequences from a million flips?
It's simple. Just find the sequence with the longest chain of heads elsewhere in the coin flip record. In a million flips, you'll probably see a maximum sequence with about 20 heads in a row, which has about a one in a million chance to occur. This means that a 40-head sequence will happen once in a million-squared coin flips, and a 60-heads-in-a-row will happen once in a million-cubed (or 1e18) coin flips. Thus, by verifying that the longest sequence of heads has about 20 head in it, I also verify that the chances of 60 heads in a row is about 1e-18. If the alternative hypothesis has any reasonable amount of probability mass near this value, most of that 1e18 would translate directly to the Bayes factor. So even when the Bayes factor is extremely large for a very strong piece of evidence, you can still get an estimate for that Bayes factor by seeing what fraction of that evidence is duplicated by chance in the population at large.
Not really. Our overall program still works. The Bayes factor for a reported testimony, or a set of such testimonies, can still be directly measured from the frequency of such reports in history. There is no need for complicated theoretical calculations of exact probabilities. That's the beauty of working from empirical, historical records: you can skip all the math and theorycrafting, and just read off the answer that reality computed for you.
Even when the testimony in question is so strong that its suspected Bayes factor far exceeds the number of possible historical records, we can still follow our program and get an estimate. Just compare the reported testimony with the closest thing that happened in history, and note the difference. This is enough to validate qualitative statements like "far exceeds 1e11". If we're willing to do a little more math, and actually model the distributions involved, we can even get a quantitative answer. In fact we will do exactly that, later in this work.
So, it basically comes down to this: you think that the evidence for the resurrection isn't good enough? Well then, start citing other, non-Christian examples in history where someone comes back from the dead. We'll see how the best of these measure up against the reports for Christ's resurrection, and then see how the Bayes factor calculated this way compares to our previously calculated value.
The New Testament, and what it would take to match its resurrection reports
Before we begin diving into specific examples of other resurrection stories in history, let us establish the comparison criteria: what would it take to match the level of evidence in Jesus's resurrection reports?
Recall that we're using the testimonies summarized in 1 Corinthians 15. This passage identifies six specific individuals or groups who personally testified to Christ's resurrection. They are Peter, James, Paul, "the twelve", the other apostles included in "all the apostles", and "the 500". Note that this is merely a summary: for many of these people, we have numerous additional records of their testimonies elsewhere in the New Testament. Notable among them are Peter's sermon in Acts 2, John's repeated appeal in the last chapters of his gospel, and Luke's report of the two disciples (not of the twelve) meeting the risen Christ on the road to Emmaus.
At this point, it's worth pointing out some of the salient features of this New Testament record. We know a great deal about how they came to be written, and there is much that can said for their veracity. For instance, we know that 1 Corinthians was written by Paul, around 50-60 AD. There is little controversy or uncertainty around either of these facts. The key resurrection passage in chapter 15 contains a formula which probably goes back to within a few years of Jesus's death. All this is generally agreed upon, even by skeptical scholars of the New Testament.
Dating the four gospels, where many additional testimonies appear in a more complete form, is more controversial. Depending to who you talk to, they're typically dated to 50-110 AD. Skeptical scholars doubt that they were written by Matthew, Mark, Luke, and John, but even they have great many things to say about their probable authors. Of course, Christians have still more things to say, including some very good reasons for accepting their traditional authorship, and earlier dates for their composition. We also know that the book of Acts - which contains still more resurrection testimonies - was written as a sequel to the gospel of Luke, by the same author. There are numerous other passages elsewhere in the New Testament, with different degrees of affirmation for the resurrection. So overall, we have a mix of many different types of testimonies in the New Testament, some of which are controversial for whatever reason.
But of course, we will not rely on anything controversial to make our case. So what would it take to "match" one of the 1 Corinthians 15 testimonies? Our plan is to compare these Christian records, under the least controversial set of assumptions allowed by the scholarly consensus, against any non-Christian resurrection stories, considered through a naturalistic process and outlook. Do any such non-Christian stories match, or at least approach, the level of evidence of the testimonies summarized in 1 Corinthians 15? This will require a careful examination of the resurrection reports from both sides. The overall quality of the evidence needs to be comparable in order to be considered a match.
Here are the minimal standards set by Jesus's resurrection, as summarized in 1 Corinthians 15:
Peter, James, Paul
To match Peter, James, or Paul's testimonies, we will require a report of a sincere, insistent, and enduring personal testimony given by a single named individual. This person must have been a public figure whose entire life (choice of profession, place of residence, etc.) was lived in complete alignment with that testimony. History must be able to locate this person with great precision, and have a good amount of information available about them.
This testimony must be reported by a well-known historical figure (corresponding to Apostle Paul), within about 30 years of the resurrection event itself (corresponding to 1 Corinthians 15). The reporter need not be the individual giving the testimony: it's enough that the report claims to represent the testimony of an eyewitness. But the reporter must have personally known the individual, and belonged to the same close-knit community.
Furthermore, this report must be strongly corroborated by some additional historical documents (corresponding to the remainder of the New Testament). These must have been written somewhat independently within about 100 years of the event, and generally accepted as true by the continuing community surrounding the resurrection event.
The twelve
To match the testimony of "the twelve", we will require a report of a sincere, insistent, and enduring personal testimony by a group of about a dozen named individuals. They must have been public figures whose entire lives were lived in complete alignment with that testimony. History must be able to locate these people with good precision, and have a good amount of information on at least some of them.
This testimony must be reported by a well-known historical figure, within about 30 years of the resurrection event itself. The reporter need not be among the people giving the testimony: it's enough that the report claims to represent the testimony of these eyewitness. But the reporter must have personally known the people in the group, and belonged to the same close-knit community.
Furthermore, this report must be strongly corroborated by some additional historical documents. These must have been written somewhat independently within about 100 years of the event, and generally accepted as true by the continuing community surrounding the resurrection event.
The other apostles
To match the testimony of the other apostles beyond the twelve, we will require a report of a sincere, insistent, and enduring personal testimony by a group of individuals. At least some of them must be named. At least some of them must have been public figures on the matter of their testimony. History must be able to locate some of these people with good precision, but not a lot of historical data is required of them.
This testimony must be reported by a well-known historical figure, within about 30 years of the resurrection event itself. The reporter need not be among the people giving the testimony: it's enough that the report claims to represent the testimony of these eyewitness. But the reporter must have personally known at least some of the people in the group, and belonged to the same close-knit community.
Furthermore, this report must be plausibly corroborated by some additional historical documents. These must have been written somewhat independently within about 100 years of the event, and generally accepted as true by the continuing community surrounding the resurrection event.
The 500
To match the testimony of "the 500", we will require a report of a sincere personal testimony by a large crowd of people. They need not be named, or be public figures, or endure in their testimony, or have any additional information known about them. But history must be able to locate these people precisely enough, so that at least some of them could be theoretically pointed out individually by a well-known figure like Apostle Paul.
This testimony must be reported by a well-known historical figure, within about 30 years of the resurrection event itself. The reporter need not be among the people giving the testimony: it's enough that the report claims to represent the testimony of these eyewitness. But the reporter must have belonged to the same close-knit community, and no further corroboration from other historical sources are necessary.
Proceeding from these standards
We can, of course, extrapolate from this set of matching testimonies. A reported testimony need not meet every single condition, if it manages to exceed expectations in some other area. But the above list should be comprehensive enough that it can serve as a metric for measuring many personal testimonies in history.
One more thing to note is the lack of negative testimony: in the above list, we seemed to have ignored anything about what to do if we find any strong evidence against a resurrection: that's because such a thing doesn't exist in Jesus's case. But we will find some such cases when we look to the non-Christian resurrection stories, and there, we must of course discount the account appropriately.
So, here's the program: we will search through world history, and examine the best non-Christian reports of a resurrection. We will examine the level of evidence behind each of them, and measure them up against one of the matching categories in the list above. We will also measure their evidence against the total evidence for Jesus's resurrection. Doing so will allow us to validate our earlier estimation of an individual's Bayes' factor, and the total amount of evidence for Jesus's resurrection.
What are we expecting? Which results would vindicate which hypothesis?
As previously stated, let us conservatively say that there have been 1e9 reportable, naturalistic deaths throughout non-Christian world history. Then a resurrection report with a Bayes factor of 1e8 would have about 10 similar cases which at least come close to matching the report in question. A better resurrection report, with a higher Bayes factor of 1e9, would be rarer and therefore be the only case of its kind, with no other comparable cases. A weak report with a Bayes factor of 1e6 would have on the order of 1000 similar cases, and so on and so forth.
I evaluated Peter's testimony by itself at a Bayes factor of 1e8, as a conservative estimate. Therefore, I expect there to be less than ten resurrection reports comparable to Peter's (or Paul's or James's) testimony. This will validate our earlier evaluation of an individual's testimony, as having a Bayes factor in excess of 1e8.
I evaluated Peter and Paul's testimonies together (including their anti-dependent nature) to have a Bayes factor safely above 1e11. Therefore, I expect that no case in naturalistic world history will match their testimonies. Even the nearest approach would fall distinctively short.
Recall that adding more evidence multiplies the Bayes factors: therefore doubling the evidence squares the Bayes factors. So, it doesn't take much evidence for the Bayes factor to go from 1e9 to 1e11. A little bit of independent evidence goes a long way. In terms of Peter and Paul, this means that the nearest approach by a resurrection report in naturalistic world history would amount to something like half of their amount of evidence, and that would be sufficient to put Peter and Paul's Bayes factor safely above 1e11.
As for the total evidence for Christ's resurrection, I evaluated that total Bayes factor to far exceed 1e11. The net amount of evidence summarized in 1 Corinthians 15 is multiple times that of just Peter and Paul's. Therefore, we would expect that there is not a single other case which comes even remotely close to matching the level of evidence for Christ's resurrection. The nearest approach by a historical, naturalistic death would fall far short of that level - not just by 30% or 50%, but by a sizable multiplicative factor.
Ah - but when we evaluate against the total evidence for Christ's resurrection, how should we weigh the six different testimonies in 1 Corinthians 15? What type of testimony is worth more? How should we evaluate a non-Christian resurrection report, if it includes an individual testimony like Peter's, and also a group testimony like "the 500"'s?
No matter - I will allow matching any of the six testimonies as counting for 1/6th of the total evidence. Essentially, I'm pretending that each of the six testimonies in 1 Corinthians 15 have equal value. This is wrong, but it's wrong in a direction that handicaps against the Christian position. What will happen is that the easiest of the six testimonies to match - which is worth less than 1/6th - would be more likely to show up in the historical record, and yet they will be given the full weight of 1/6th. So any errors in the evidence-level assignment due to our metric can only be favorable to the skeptic's case. Any pro-Christian conclusions we come to will therefore have an extra margin of assurance.
All this gives us a clear goalpost as to what observations would validate our previous calculations. Making those observations will show that an individual testimony like Peter, James, or Paul's is worth a Bayes factor of at least 1e8, that Peter and Pauls testimonies together (including their anti-dependence factor) is worth well above 1e11, and that the sum total of evidence for Christ's resurrection is far in excess of 1e11.
Now we're finally ready to look at the non-Christian historical records. Let's start.
The other historical records:
Fortunately, skeptics of Christ's resurrection have done some of the early legwork for us, in that they compile lists of purported people who have been said to be like Christ for one reason or another. These include a number of people who are said to have been raised from the dead. Let us look at a representative sample from such lists.
Apollonius of Tyana:
Apollonius of Tyana is sometimes compared to Christ because they were both philosopher/preachers in first century Rome, to whom miraculous powers are attributed. Wikipedia has a list of similarities between Jesus and Apollonius, which includes a wondrous birth, the ability to heal the sick and raise the dead, a condemnation by Rome, and an ascension into heaven. That sounds pretty similar, no? So how does the evidence for Apollonius's "resurrection" hold up?
Pathetically. Most of the information on Apollonius comes from Philostratus, who was paid to write a biography of Apollonius well over a hundred years after Apollonius's death, and after Christianity was already a thing. This biography only "implies" that Apollonius underwent heavenly assumption. Furthermore, the chief primary source for this biography is one Damis, a disciple of Apollonius, who is unknown outside of this biography. And to top it off, Philostratus specifically writes that Damis had not recorded anything about Apollonius's death. The stories of his death and supposed heavenly assumption are in a part of the biography that are filled with 'some say this, some say that' stories, which, by the author's own admission, he wrote because he felt that his story needed to have a natural ending.
So, the evidence for Apollonius's "resurrection" comes down to one author, who wrote more than a hundred years after the event, who says that he's getting his information second-hand from a Damis that nobody else has heard of, who then explicitly says that the "resurrection" bit - which is only implied - doesn't even come from Damis.
Compare that to the evidence for Christ's resurrection: 1 Corinthians 15 was written within a couple decades of the event, and it contains a creed that was formulated mere years after the resurrection. It claims to represent the the personal, first-hand testimonies of the people who have seen the risen Christ. We know that these witnesses said that it really happened, and that it transformed their own lives: each of these disciples appear in multiple other sources, and bear the same witness about Christ's resurrection in those sources.
So... now we're suppose to compare the strength of the evidence between these two? Well, let's see. Remember our previous criteria, about what it would take to "match" 1/6th of the evidence in 1 Corinthians 15. Can we say that maybe Damis's testimony about Apollonius's resurrection matches the testimony of Peter, James, or Paul? Well, no. Damis never even made that testimony, nor is he anything like those three individuals on the quality of historical information we have on him. So then, all that's left as evidence is "some people say that Apollonius rose from the dead", stated more than a hundred years after the fact?
That isn't much evidence. There is nothing here that matches any of the individual testimonies of 1 Corinthians 15, and the best evidence by a group is just a vague report about how "some people say..." that Apollonius lived on after death, which is essentially the weakest form of evidence possible for a group of people. Overall, everything here falls far short of matching any of the six corresponding components in 1 Corinthians 15, let alone matching the whole thing.
Zalmoxis:
Next, let us consider Zalmoxis, whom Herodotus writes about in his "Histories" as a divinity in the religion of the Getae. Herodotus wrote that Zalmoxis's followers believed they have a form of immortality in him, and performed a kind of human sacrifice to communicate with him through death.
According to Herodotus, he was told by certain non-Getae peoples that Zalmoxis was really a man - that he was teaching his countrymen some philosophy, but then hid himself in a secret underground housing for three years while people thought he was dead. He then came back out and showed himself alive, and this caused the people to believe his teachings.
And... that's it. That's the substance of this Zalmoxis and his "resurrection". I'm not even summarizing that much - the text in Herodotus is hardly longer than the above paragraph. Apparently this is one of the best examples that the world can come up with when asked about non-Christian resurrection stories. And yes, some people really have tried to link this "resurrection" to Jesus's resurrection, in their attempt at discrediting Christianity. This, in spite of the record having no witnesses testimonies of any kind, nor even a group of people who can clearly be said to believe that someone came back from the dead.
Again, using the standards derived from 1 Corinthians 15, how does this measure up against the evidence for Christ's resurrection? Is anything about Zalmoxis's "resurrection" comparable with the testimonies of Peter, James, or Paul? Well, no. Zalmoxis has no witness testimonies, period - let alone any named witnesses among historically known persons. This means that nothing about Zalmoxis is comparable to the testimony of the apostles as a group, either. At the end of the day, all the evidence for Zalmoxis's "resurrection" comes down to "some people might have said that a god, who might have been a real person, might have come back from the dead". Note that all the "might have"s in that sentence are part of the historical evidence. It is not an external skeptic injecting doubt into the story, it's actually how the story is handed down to us through history.
So... I would again say that the evidence here is negligible. There is nothing here worth comparing to anything in 1 Corinthians 15.
Aristeas:
Let's next look at Aristeas, who is another character in Herodotus's "Histories". He is said to have been a poet. The "Histories" relate how Aristeas "suddenly dropt down dead" one day (in front of just one witness), but then his body could not be found and he was seen alive - once close to the time of his death, and then seven years later, when he appeared in another town and wrote a poem.
Here's the thing about this story: it was already at least 240 years old when Herodotus was telling it. Then, Herodotus says that some people say that Aristeas appeared again (as a "ghost" or an "apparition") after those 240 years, and instructed these people to build an altar to Apollo and a statue of Aristeas himself.
Again, that's about it. The whole story only takes up a couple of paragraphs in Herodotus's "Histories". Now, it's not quite clear that a "resurrection" had taken place - the first part of the story sounds more like a fainting or a disappearance, and the second one is called a "ghost" or an "apparition" by the people who were suppose to have seen it, who presumably had no means of personally identifying Aristeas. But let's ignore that for now. What kind of evidence - what kind of witness testimony - do we have for this story, and how does it compare to the story of Christ's resurrection?
Well, once again we have no named witnesses. The first part of the story is at least 240 years old at the time of the telling - so no personal witnesses are even possible. The second part, where a ghost or an apparition instructs people to build an altar and a statue, may be a bit more credible. We seem to at least have a group of people who were instructed to build a specific altar and statue, and Herodotus might have conceivably met the individuals who claimed to have personally received these instructions. On the other hand, they are never identified more specifically than "the people of Metapontion", and it's unclear whether this is simply a story that the Metapontines told about their altar and statue. Furthermore, it's not even clear how long ago this was supposed to have happened - the story about the apparition might as well have happened another 240 years ago from the time that Herodotus relates the story, judging from the scant details.
So, once again the testimony evidence here only turns out to be of the "some people say..." kind. The closest thing we can relate this to is the testimony of the 500 witnesses in 1 Corinthians 15, but it again falls distinctly short of it, with the rather shadowy nature of the "apparition", the uncertainty about whether Herodotus has any specific primary witnesses in mind, and the large spans of time involved.
Mithra:
How about we look at some ancient gods? Jesus is often compared to the gods in other religions, but can any of them actually serve in our comparison of historical evidence for a resurrection?
Mithra, for instance, is a god in the Persian religion of Zoroastrianism, who then inspired a Roman mystery religion. He often appears on lists of gods that Jesus was supposed to have been copied from. But... um... it seems that he was never actually said to have been a human, or any kind of a historical figure, in either the Persian or the Roman variants. He doesn't even die, let alone rise from the dead, even in his mythologies. Furthermore, any specific details or even general plot points is notoriously difficult to extract from any Mithra mythology. The Roman version of Mithra was worshiped in a mystery religion, and none of their written narratives or theology survive - we only have some iconography to glean what we can of this Mithra. In the Persian version, Mithra is mentioned in some hymns (Yashts), which are again very short on details, mythology, or narrative. In all cases, he is always presented as a mythic entity, and the scant stories about him are always framed in that context.
So, on his comparison with Jesus, we can safely say that there is no evidence for Mithra's resurrection. Indeed such a claim is never even made, or even dreamt of.
Horus and Osiris:
Horus, an ancient Egyptian god, along with his father Osiris, are some more gods who are sometimes compared to Jesus. As with Mithra, all of the stories concerning these gods take place on a purely mythological level, and they have nothing that allows us to locate them in history. For our purposes, it's clear that their story presents no evidence for a historical resurrection. But at least Osiris has a mythological story where he comes back after being murdered, and there is a story where Horus, as a child, recovers from a fatal scorpion sting. So, it's at least true that "some people say..." that Osiris and Horus and came back from the dead. But it's impossible to locate the original among such group of people, who might have claimed to have been the personal witnesses to these events - all ancient sources (Pyramid Texts, Palermo Stone, Metternich Stela, etc.) which mention these stories always present it something that took place a long time ago, in an mythic age.
Needless to say this fails on all points of comparison in matching the evidence for Christ's resurrection.
Dionysus:
Dionysus is another god, this time from the Greek pantheon, who is superficially compared to Jesus. Yes, there is a mythological story where he is killed as an infant then re-incubated in Zeus's thigh - but none of the sources that mention this mythology is of any help in locating them in history. Dionysus's situation with regards to his "resurrection" is therefore similar to that of Osiris or Horus - there is virtually no historical evidence for his "resurrection".
As with Horus and Osiris, "some people say..." is the most that can be said for the case for Dionysus's resurrection.
Krishna:
We now come to Hinduism's Krishna, who's another god that's sometimes compared with Jesus. He's said to be have been the incarnation of Vishnu, who is either the supreme god, or one of three or five most important gods, depending on the specific tradition in Hinduism.
Krishna has perhaps a greater claim to a real, historical substance compared to the other gods we've covered. For starters, he is at least said to have been born as a human. He is said to have gotten married and ruled kingdoms and fought battles. There is a great deal that is said about Krishna - but we are, of course, primarily interested in the story of his death and "resurrection".
The main literary sources we have on this part of Krishna's life are the Mahabharata and the Srimad Bhagavatam. They tell the story of how Krishna, at the end of a long and eventful life, intended to leave the world. He was then shot by a hunter named Jara, with an arrow through the foot. This marked the end of Krishna's life, for thereafter he immediately ascended to go to his own abode, leaving earth.
So, what are we to make of this "resurrection" story? What kind of evidence is there for it? Let us first try to establish the setting. These stories take place in ancient India, and Krishna is proposed to have lived some time between 3200 and 3100 BC, although there are some wildly differing estimates. These are quite large uncertainties, from a very long time ago - right at the edge of pre-history. These issues, by themselves, might not cause too much concern - until we attempt to date the writing of the Mahabharata, which contains these stories.
Dating the Mahabharata is tricky - it is a massive work, composed of multiple layers. Current scholarship estimates that the oldest layers are from around 400 BC, and the origin of the stories within it can perhaps be extended back to 1000 BC. In other words, the stories of Krishna were, at best, already thousands of years old at the time that they were recorded. Therefore, no personal, firsthand testimony to Krishna's death and ascension are possible in this work.
Okay - but what if we ignore the scholarship, and and go with the Hindu tradition which says that the Mahabharata was authored by the legendary sage Vyasa? Unfortunately, this doesn't help things at all. We know little about a historical Vyasa. When did he live? When did he write? We can no more anchor him in history than we can Krishna.
Complicating matters further is the story structure of the Mahabharata. You see, the death and ascension of Krishna is not just told as a story; it is framed as a story being told by Vaisampayana (a student of Vyasa) to the king Janamejaya (supposedly a great-grandson of a character in the Mahabharata), many years after the fact. But that's not the end of it - this story is further framed as a story being told by Ugrasrava Sauti, even more years later. So, the story of Krishna's ascension is a story (about Krishna), within a story (being told by Vaisampayana), within a story (being told by Ugrasrava Sauti), within a work (the Mahabharata itself, which was presumably written down some time afterwards). All this "story-within-a-story" structure sounds like a device for saying "once upon a time...", and makes the story sound like something told about "a friend of a friend". But let us ignore that for now. Even if we were to take the Mahabharata entirely at face value - an outlandishly generous acquiescence - we would still be forced to conclude that this story was already incredibly old at the time of the recording, and its content disqualifies itself from being considered a primary account, due to its story-within-a-story structure. Again, no personal testimonies are possible.
But - what if the dates for Krishna's life are mistaken? What if he lived more recently than in the 4rd millennium BC, and the portion of the Mahabharata which contains his ascension were written closer to the actual event, and the rest of the Mahabharata, including the story-within-story structure, was built up later? Well, that's a lot of "what-if's" - and while that does get the text closer to the event, it's still of no help in solidly placing Krishna in history, or producing personal testimonies from any witnesses to his ascension.
Going to the Srimad Bhagavatam instead of the Mahabharata doesn't help here - for the Srimad Bhagavatam was written even more recently than the Mahabharata. Modern scholarship places its composition as some time between 500 to 1000 AD, and it references parts of the Mahabharata. In fact, its other name - Bhagavata Purana - means "Ancient Tales of Followers of the Lord". The work itself acknowledges that these are "ancient tales", right there in the title. It cannot possibly produce the kind of testimonies we're looking for.
Let's again compare all this to the evidence for Jesus's resurrection, recalling the important facts. 1 Corinthians was written a mere 20-30 years after the event. The creed within it comes within several years of the event itself. Furthermore we have numerous records elsewhere in the New Testament of people claiming to have personally seen the risen Christ. These are stark differences compared to the ascension of Krishna. We have time gaps of years compared to millennia, and personal, firsthand testimonies instead of a story about a story about a story about an ascension. It may be that Krishna was a real person who once lived a remarkable life. It may be that the Kurukshetra War actually took place. But in judging the amount of evidence for Krishna's ascension, there can be no real comparison to the evidence for Christ's resurrection.
But in the end, we still need to evaluate the level of evidence for Krishna's ascension. Well, we can certainly say that some people say that Krishna "rose from the dead". But we cannot historically locate any group of people who first personally testified to this fact, like we can with the 500 witnesses in 1 Corinthians 15. Nor can we find any group of witnesses corresponding to the apostles, or to the specific named witnesses in 1 Corinthians 15. In the end, we just seem to have the story in the Mahabharata, with the version of the story in Srimad Bhagavatam being a later telling of the same story.
So we have the usual "some people say..." level of evidence, although there is perhaps something to be said for the sheer volume of the works about Krishna. But at the end of the day, this still falls distinctly short of the testimony of the 500 witnesses for Christ's resurrection.
Bodhidharma:
Let us now turn to some figures from Buddhism who are said to have appeared after their deaths.
Bodhidharma is the Buddhist monk credited with bringing Chan Buddhism to China, some time around the 5th century AD. Here is Wikipedia's summary of the legend surrounding his death:
Three years after Bodhidharma's death, Ambassador Sòngyún of northern Wei is said to have seen him walking while holding a shoe at the Pamir Heights. Sòngyún asked Bodhidharma where he was going, to which Bodhidharma replied "I am going home". When asked why he was holding his shoe, Bodhidharma answered "You will know when you reach Shaolin monastery. Don't mention that you saw me or you will meet with disaster". After arriving at the palace, Sòngyún told the emperor that he met Bodhidharma on the way. The emperor said Bodhidharma was already dead and buried and had Sòngyún arrested for lying. At Shaolin Monastery, the monks informed them that Bodhidharma was dead and had been buried in a hill behind the temple. The grave was exhumed and was found to contain a single shoe. The monks then said "Master has gone back home" and prostrated three times: "For nine years he had remained and nobody knew him; Carrying a shoe in hand he went home quietly, without ceremony."
So, that's something. We not only have the usual "group of people who believe" that Bodhidharma rose from the dead, but also a named figure, one "Ambassador Sòngyún of northern Wei", who at least sound like a historical person. So, how should we evaluate this story?
As before, we first ask where this story comes from. It turns out that the source for this story is the Anthology of the Patriarchal Hall, which was compiled in 952 - about 400 years after Bodhidharma is supposed to have died. Again, this is far outside a human lifetime, and that makes it impossible to find the kind of personal testimonies of historical individuals that we're looking for.
As for "Ambassador Sòngyún of northern Wei" - well, it turns out that he really is a historical person - a Buddhist monk who was sent into India to acquire some Buddhist texts, some time around 520. But this does not really help the case for Bodhidharma's "resurrection", because none of the texts that mention Song Yun or his journey mentions this "resurrection". The event therefore seems to be a later, legendary addition.
The other sources on Bodhidharma, many of which are earlier than the Anthology of the Patriarchal Hall, also force us to draw the same conclusion. None of them mention this story of Bodhidharma "going home". It is clearly a later, legendary addition, and Wikipedia has no qualms about labeling it as such.
Let's now try to match this up to the testimonies in 1 Corinthians 15. First, there's the usual "some people say this happened" dimension to the story. As for "Ambassador Sòngyún of northern Wei", having a named, real, historical witness would match up to a testimony from Peter, James, or Paul, and would count as a full 1/6th of the total evidence in 1 Corinthians 15 - except that this witness is named 400 years after the fact.
This may still count as some non-negligible fraction of that 1/6th, but nearly all of this gets wiped out by the strong evidence against the story from the lack of mention in the earlier sources, indicating that this whole story is a later, legendary addition. In the end, the level of evidence for Bodhidharma's "resurrection" can't amount to anything more than the "some people say..." level.
Puhua:
Puhua (known as Fuke in Japan) was a Chinese Buddhist monk, who supposedly lived around 800AD. He, too, is said to have not really died. He may or may not have been a real individual. If real, he was a student of Linji (known as Rinzai in Japan), who was another Chinese Buddhist monk, who founded the Linji school of Chan Buddhism.
Here's the story of Puhua/Fuke's death and "resurrection" as told in the Record of Linji, quoted by Wikipedia:
"One day at the street market Fuke was begging all and sundry to give him a robe. Everybody offered him one, but he did not want any of them. The master [Linji] made the superior buy a coffin, and when Fuke returned, said to him: "There, I had this robe made for you." Fuke shouldered the coffin, and went back to the street market, calling loudly: "Rinzai had this robe made for me! I am off to the East Gate to enter transformation" (to die)." The people of the market crowded after him, eager to look. Fuke said: "No, not today. Tomorrow, I shall go to the South Gate to enter transformation." And so for three days. Nobody believed it any longer. On the fourth day, and now without any spectators, Fuke went alone outside the city walls, and laid himself into the coffin. He asked a traveler who chanced by to nail down the lid. The news spread at once, and the people of the market rushed there. On opening the coffin, they found that the body had vanished, but from high up in the sky they heard the ring of his hand bell."
As before, we want to evaluate the evidence for this story, and begin by inquiring about the source of the story.
We've said that this story comes to us through the Record of Linji - a work that was not consolidated until more than 250 years after Linji's death in 866. Puhua, if he was real, died before Linji - as the story itself makes clear. Therefore, this story about Puhua's death and "resurrection" was recorded more than 250 years after the event itself. Again, the large gap, which far exceeds a human lifetime, makes it impossible for us to find anything like the personal testimonies of historical individuals.
One day Puhua, carrying an armload of coffin-planks, went about town bidding farewell to the townspeople, saying, “I’m leaving this life.” People gathered in crowds and followed him out of the east gate. He then said, “No, not today!” The second day he went to the south gate and the third day to the west gate. By that time fewer people were following him, and not many believed him. On the fourth day he went out of the north gate, but no one followed him. He dug a tunnel, lined it with bricks, and died therein.
This is, of course, essentially the same story as the one found in the Record of Linji - except there is no resurrection. So, Puhua died, supposedly in 840 or 860. We then have the Anthology of the Patriarchal Hall, written in 952, which mentions Puhua's death but says nothing about a vanished body or a resurrection. We then finally come to the Records of Linji, which was consolidated after 1100, where a resurrection shows up attached to the end of the same story as the one in the Anthology of the Patriarchal Hall. We furthermore know that the Anthology of the Patriarchal Hall is not shy about putting in resurrection stories, since it included one for Bodhidharma. So, why does it not include Puhua's resurrection story? Because the story did not exist yet. The obvious conclusion is that Puhua's "resurrection" is a legend developed after 952.
Again, it's difficult to compare something like this to the evidence for Jesus's resurrection in the New Testament. Nothing in the New Testament makes any sense without Jesus having risen from the dead. The whole corpus, from beginning to end, testifies to Christ's resurrection, without ever wavering from that truth. Trying to attach a false "resurrection" to a naturalistic "historical Jesus" could never have produced the infusion of that resurrection permeating the whole collection of documents.
In contrast, the only thing we can say for Puhua's resurrection is that "some people say..." it happened. As with all of the other cases we've examined, this fails to even come close to matching any of the six sets of testimonies in 1 Corinthians 15.
Our previous calculations are fully validated
So, let us summarized these non-Christian resurrection accounts. The following table shows the level of evidence associated with each of their "resurrection" stories.
| Name of the person | The level of evidence |
| Apollonius of Tyana | "some people say...", reported more than 100 years later in a large work. |
| Zalmoxis | "some people say..." |
| Aristeas | "some people say...", associated with an alter/statue of him in Metapontion. |
| Mithra | None. He's not said to have been resurrected. |
| Osiris | "some people say..." |
| Dionysus | "some people say..." |
| Krishna | "some people say...", reported in a very large work. |
| Bodhidharma | "some people say...", cites a historical person as a witness. |
| Puhua | "some people say..." |
You'll notice that they're all just variations around the "some people say..." level of evidence. This level of evidence is quite weak. It's nothing special. We've just seen that it occurs multiple times throughout world history, even under naturalistic assumptions. The strongest evidence of this type may be identified as something that stands distinctly as the best, as something that occurred only once in non-Christian history. It's doubtful that any of the above reached this level, as none of them are distinctly above the rest. But even this "only once" level would fall distinctly short of the 500 witnesses testifying to Christ's resurrection, as nothing like it, or even remotely comparable to it, has ever occurred even once outside of Christianity.
So, the "some people say.." level of evidence falls far short of the testimony of 500 witnesses, which in turn is probably the weakest of the six components in 1 Corinthians 15, as it was the closest one to being replicated in naturalistic history. The total amount of evidence for Christ's resurrection is therefore at least six times greater still.
Essentially, there's nothing in world history which can come anywhere near matching up to any one of the six components in 1 Corinthians 15. Here's how this looks like in a histogram:
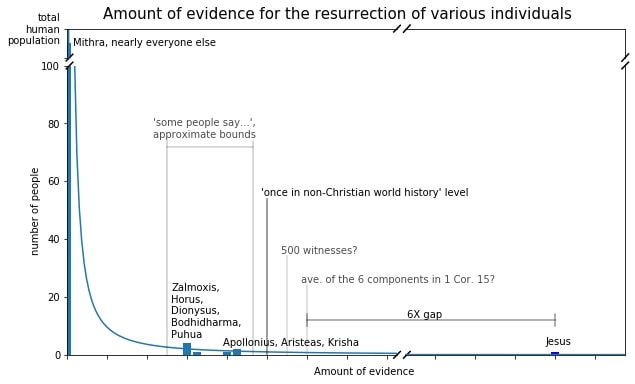
What does all this tell us? Quite a bit.
Let us recall our purpose in making these historical comparisons: we wanted to verify our Bayes factors for the evidence involved in Christ's resurrection.
The first part of our plan was to look for non-Christian resurrection testimonies matching any one of Peter, James, or Paul's testimonies. The number of such testimonies would determine their Bayes factor, and give us a independent way to validate our estimate of 1e8 as the Bayes factor of a single human testimony.
As we just saw, there was not a single instance of such testimony in any non-Christian resurrection stories among the ones we investigated. None even came remotely close. There may perhaps be one such testimony if we exhaustively investigate the entire historical record, but even that's doubtful, as we've already looked at the likeliest candidates, and we're already very much scraping the bottom of the barrel.
So, it turns out that if anything, 1e8 is an underestimate for Peter, Paul, and James's testimonies. The full-blown set of conditions associations with their testimony strengthens them significantly beyond just a sincere human testimony. Our best guess is that there might be a single non-Christian testimony that approaches one of theirs, but it's unlikely. Given our earlier estimate of 1e9 reportable deaths, that puts Peter, Paul, and James's testimonies, individually, at a Bayes factor of around 1e9 or more. In fact, since all this can be also said of the 500 witnesses, we know that the 500 must have a Bayes factor of 1e9 or more, and that the named witnesses must have a greater Bayes factor still.
This also validates our estimate that Peter and Paul's testimonies, taken together with their anti-dependence considerations, have a Bayes factor safely above 1e11. We could not find even a single testimony matching either Peter or Paul's testimony individually, let alone two such testimonies, or two such testimonies where the individuals started out as enemies. As if that wasn't enough, we could not find even a single case where an initial skeptic of a resurrection changed his mind, even in a mythical story. No matter how one slices it, Peter and Paul's testimonies together are far above what might have appeared naturalistically in world history. There is nothing that matches them and nothing that can even come close to them. This fact verifies our claim that just these two testimonies together are enough to make Jesus's resurrection quite probable.
Lastly, we wanted to compare the total evidence summarized in 1 Corinthians 15 with the "nearest approach" by a non-Christian resurrection story in history. As we've seen, even the best non-Christian resurrection stories, with the greatest amount of evidence behind them, fell far short of the evidence in any of the six components in 1 Corinthians. Even the weakest of the six components has been demonstrated to be much greater than that, with a Bayes factor of at least 1e9, and the total evidence for Christ's resurrection is at least six times greater in turn. If we assumed independence, this would result in a Bayes factor of at least 1e54 at a minimum, and likely much larger. This value is so large that it's essentially impossible to reduce it below 1e11, even if you factor in dependence, even when crackpot theories are in play. We will later demonstrate this with a full calculation. But for now, we can qualitatively say that our earlier claim is validated: the total amount of evidence for Jesus's resurrection is not just greater than anything that was naturalistically generated in history. It is not even just distinctly greater by a significant margin. No, it is greater by a large multiplicative factor, to the point where the two are hardly comparable. Beyond any reasonable doubt, Jesus Christ rose from the dead.
What, if anything, is wrong with the previous argument?
It is natural and proper to critique an argument. Some critiques are weak, brought on by those who are looking to provide the thinnest veneer of intellectual justification for their unbelief. Others may actually succeed in countering the argument. Therefore, critiques must be critiqued in turn, and the original argument's mettle can be thereby ascertained.
Is the prior too large, especially for a supernatural event?
One possible class of objections would try to argue that the prior odds for the resurrection wasn't small enough. One may say:
"It's not just that people don't rise from the dead. NO supernatural claim of ANY KIND has EVER been validated in a controlled setting. Therefore the prior odds for the resurrection must be smaller than the value used in the calculation."
Well, let's just give away everything this objection asks for. Remember, our starting point was to take every human to have ever existed (1e11), and say that they all died and stayed dead without a resurrection. But now, in addition, let's say that every one of these 1e11 people were qualified scientists, who each published 99 papers in a peer-reviewed scientific journal, with each paper reporting an empirical observation which conforms to a naturalistic worldview. We will just ignore the fact that this level of testing simply hasn't been actually done.
This background of 1e13 observed naturalistic events would give us a prior odds of 1e-13 for our event under consideration - the supernatural resurrection Jesus Christ. Meaning, even after that absurd assumption in favor of naturalism, the prior odds only changed from 1e-11 to 1e-13 - woefully inadequate for materially changing any of our previous conclusions.
Shall we turn it up another notch? Say that the 1e11 people, in addition to each publishing 99 papers, also each make 100 supernatural claims which are later debunked - they're eventually all explained by naturalism. That would make for 200 confirmed naturalistic empirical observations per person, which only bring the prior odds down to 0.5e-13 - a meaningless change.
Remember, just Peter and Paul's testimonies have a Bayes factor safely and distinctly above 1e11. The total evidence in 1 Corinthians 15 is much, much greater still. A Bayes factor like 1e-13 presents no problem for this amount of evidence.
How about yet another way to see the futility of this objection? The historical record again gives us a completely different way to approach this problem. Remember, there is no non-Christian resurrection report which matches any part of the report in 1 Corinthians 15. Well, does the skeptic fare any better if we expand our examination from "non-Christian resurrection reports" to "non-Christian miracle reports"?
As we will later see, they do not. Even with this expansion to any kind of miraculous reports, there are hardly any that come close to matching, say, Peter's testimony by itself. This means that the rest of the argument follows through unchanged: Peter's testimony by itself is enough to negate nearly all of the small prior, Peter and Paul's together is enough to safely and significantly overcome it, and all of 1 Corinthians 15 completely overwhelms it.
The inherent problem with this kind of approach - of trying to lower the prior by citing more numerous events in favor of naturalism - is that it's fundamentally an additive process. On the other hand, the report of a new testimony can increase the Bayes factor exponentially. Trying to outpace an exponential process with an additive one is a losing proposition. It's like trying to stop an exploding atomic bomb by removing the uranium atoms one by one. The prior for a supernatural event - almost regardless of how many events you cite in favor of it - is bound to be overwhelmed by a report of human testimony.
In fact, a moment's reflection shows that reportage must have an enormous Bayes factor, which easily overcomes the small prior against a previously unobserved phenomena. Otherwise, science itself would be impossible. For what do scientists do when they observe something new? Do they just say "that can't happen because it goes against established science"? Of course not. They report it, by publish a paper in a journal. If these reports did not largely negate the low prior odds of the new phenomena - if their posteriors were still, say, 1e-4 or below - then nobody would bother to read these journals. And without an effective way to share new observations or results, science would grind to a halt.
An aside: confirming general relativity
This idea, that science itself depends on reporting previously unobserved phenomena, is important enough to merit an extended illustration.

Say that you're living in early 20th century. You're smart and rational, but you're not a scientist. You lack the expertise to evaluate specific scientific claims, and you're not that interested anyway. But one day, you happen to hear, in passing, something about this guy with a crazy hairdo, making crazy claims of upending hundreds of years of the best-established science in the world. The specific claims are all nonsense, too: time travels differently at different places, light beams can curve in the vacuum of space, and apparently something special's suppose to happen at next total solar eclipse. You're not even sure what you heard was suppose to be about real life. Was that some science fiction story about time travel? Or the mythology of an astrological cult?
Note that, from your point of view in the early 20th century, this situation has all the key elements of a supernatural event: this crazy-haired guy's claim contradicts established science, has never been observed before, and goes against all common sense. In fact, a supernatural event, like the resurrection of Jesus, can be thought of as a kind of scientific revolution. They both say: "the universe does not work the way you thought it did. It works in this other way, which seems crazy to you for now." And if you're willing to abandon the nebulous and arbitrary distinction between what's "natural" and the supernatural, you'll see that the analogy is quite exact.
At any rate, you don't pay much attention to this Einstein fellow, figuring that you can't be bothered to keep track of all the crazy people out there. But one day, you read the following headline in a newspaper:
LIGHTS ALL ASKEW
IN THE HEAVENS
Men of Science More or Less
Agog Over Results of Eclipse
Observations.
EINSTEIN THEORY TRIUMPHS

You quickly skim through the article, and realize what it is: a report on the experimental confirmation of a prediction of general relativity - specifically, the bending of starlight, observed as they passed by the sun during a total solar eclipse.
At this point, you haven't spoken to Einstein. You haven't spoken to Eddington, who conducted the experiment. You don't recognize their names, you haven't looked into their work, and you wouldn't understand it even if you had. You haven't even had time to realize that the newspaper you picked up was the New York Times. There is nothing about the trustworthiness of famous scientists, or of the scientific method, or of newspaper journalism at work here. All you've done is scanned through some words in a report, in just a few minutes.
And yet, at this point your posterior odds for the bending of starlight should be something pretty close to 50-50. Even the other predictions of general relativity, along with the essential correctness of the theory as a whole, should have a posterior within spitting distance of even odds. You certainly can't think that it's anything too small - almost certainly bigger than 1e-4 - unless you're ready to cite an inversely many number of false groundbreaking scientific reports for every true one I can cite.
Consider what this means: the report you read caused you to update your belief in Einstein's claims. Their odds went from a tiny number - something corresponding to the odds of a supernatural claim or a scientific revolution - to something close to 1e0, meaning their Bayes factor must be close to the reciprocal of the prior. At this point, it hardly matters how unlikely you think such events are. This example demonstrates that a single report, skimmed over quickly, must have at least enough Bayes factor to mostly overcome that prior.
Multiple reports can then push the odds safely over 50-50. In fact, this suggests a rule of thumb regarding human testimony: any postulate, regardless of how small its prior odds may be, should be considered basically true on the testimony of two qualified, independent witnesses. The first testimony eats up the prior odds, and the second one pushes it over the top. Now, exactly who counts as a "qualified witness" will vary depending on the nature of the postulate. For something like general relativity, it would be qualified scientists, like Eddington and Einstein. For something like the resurrection of Jesus, it would be the people who were familiar with his death and witnessed his resurrected form in person afterwards.
It's easy to see that this rule of thumb fulfills multiple checks for self-consistency and common sense. For instance, it backs up a line of reasoning I used near the beginning: the testimony of Peter and Paul is enough to establish that Jesus rose from the dead. It also echos the biblical injunction in criminal justice, that a charge should be established only the evidence of two or more witnesses. So this rule is validated in multiple ways, and in turn validates that Jesus rose from the dead.
Nor should any of this surprise any scientist. After all, this is how science works. Eddington's confirmation of general relativity is the epitome of the scientific method in operation. The skeptic's attitude - of "that can't happen because it goes against established science" - is far from a scientific mindset, and in fact would make scientific progress impossible. And as we have just seen in this archetypal example, a simple report is sufficient to mostly negate a small prior, even for an unprecedented event.
(more material) next leveling: (a + b)**(-5/2) prior, looking at parameter space reduction in physics
upper limit of any human theory: 1e-11 * 1e-4 or so?
"But Science!"
Here is another objection along the "prior is too big" line.
"But science says that miracles can't happen; so whatever prior odds value you've set for the resurrection must have been too big to start with. If the conclusion to the calculation is that the resurrection actually happened, we must reduce the prior odds, so that we can arrive at a rational, scientific answer."
One wonders at how anyone can invoke "science" after abandoning empiricism and ignoring mathematical reasoning. This kind of statement betrays a willingness to pay lip service to math, reasoning, and science, while ignoring the conclusions that these fields actually lead to - all for the purpose of clinging to a bankrupt preconceived notion.
For instance, I have seen numerous skeptical arguments about miracles that mention Bayes' theorem and their prior odds. I have not seen a single one of these put an actual, numerical value to this prior odds. Among all the ones that I've seen, the argument has ALWAYS been "and since this number is going to be so small, it might as well be zero, although the value isn't actually, absolutely zero". So they claim to acknowledge that the prior odds can't be zero, while the argument functions as if it were zero in all circumstances. Thus they pay lip service to probability theory to gain a veneer of respectability, while ignoring it in practice to reach their preconceived conclusions.
You must actually do the math. Use Bayes' rule. At the very least, don't just bring it up only to have your biases negate the whole point of using Bayesian reasoning. Try to assign actual values to the various probabilities and likelihoods, even if they're just order of magnitude estimates. Base these values on some kind of empirical data. And most importantly, don't just reject the conclusion because it doesn't agree with your preconceived notions, or fiddle with the numbers to arrive at the your pet conclusion.
Can human testimonies be trusted?
"The Bible is something that some people just wrote down, right? In general, you can't trust people. Human testimonies are worthless", says the naive skeptic. Now, I should be charitable, and assume that such a person is consistent in their view. Then they ought to distrust every expression of human thought they have ever read or heard in any medium. Their entire knowledge base ought to have been established via personally conducted, direct scientific experimentation. One wonders how their visits to the doctors go, or what it was like for them to learn to dress themselves.
Perhaps this objection could be tempered by saying that human testimonies aren't entirely worthless, or that testimonies of certain types can sometimes be trusted. If you're in this camp, I certainly hope that you keep your mind open when someone comes to you with ample, empirical evidence from multiple sources using many independent lines of thought about exactly how to quantify the strength of a human testimony.
So, human testimonies cannot be dismissed out of hand simply because they're human testimonies. But this detour does raise the issue where testimonies of a certain type, made under certain conditions, may be less reliable. Let's see if there's any tenable objections along this line of thought.
Can the New Testament be trusted?
A fairly standard diatribe against the Christian scriptures may go like this:
"The New Testament is not historically reliable. It's full of exaggerations, myths, discrepancies, contradictions, and theological agendas, with little concern for what actually happened. You therefore can't use them as any kind of evidence."
Now, I obviously disagree about the New Testament being unreliable, but that's not important right now. My argument makes no particular appeal to the accuracy of the New Testament: it only depends on the mere existence of these documents, which say what they say. Recall the argument in the previous chapter, of comparing reports of Jesus's resurrection to others throughout history: it only required empirically quantifiable measurements, such as the number of witnesses, the time between the event and the testimony, and the amount of historical material we have for these witnesses. And from only these, we got a Bayes' factor of greater than 1e9 for each of the six sets of witnesses in 1 Corinthians 15.
As an aside, you may wonder how the record of a testimony can have a greater Bayes factor (1e9) than the testimony itself (1e8). As a matter of mathematics, I could just point out that the numbers I've given are merely lower bounds, but there's also something else going on here: the record of a testimony really can have greater weight than the testimony itself. It's one thing to claim that you're the smartest person in the world; it's quite another to have someone else - especially someone sympathetic to your case - record that you said it. Likewise for the New Testament: sure, the recording of personal testimonies in the New Testament might have introduced a variety of errors. But the extra credibility needed to convince others to record, preserve, and transmit such reports, especially in light of the intense persecution that early Christianity endured, enhances the reliability of such records in equal or greater measure - and our calculations bear this out.
But again, the details here don't matter for the main argument. You don't have to believe anything about how well the New Testament preserved the personal testimonies. We may all have our private opinions on how or why the New Testament records have the Bayes factor they do, but none of them enters the actual calculations. Our conclusions only require a applying straightforward statistics to empirical, historical records.
So the claim that "the New Testament is not historically reliable" simply fails to be relevant, as we've never allowed such subjective judgements to enter into our reasoning in the first place.
Could the disciples have been genuinely mistaken?
One more objection might go like this:
"1e8 is a ridiculously large Bayes factor for people's testimonies. People make mistakes all the time. Do you not know, for instance, how inaccurate eyewitness testimonies are? It is far more likely that the reports of Jesus's resurrections are mistakes of this type, rather than an accurate depiction of the events."
First, let's go over a few things before we tackle the specific issue on the reliability of eyewitnesses. The value for Bayes factor that I used - 1e8 - is derived from the strength of a human testimony in general, with relatively few conditions attached to it. It is the typical value to be assigned for someone saying "yes, this really happened", in circumstances similar to the disciples after the resurrection. Of course, if you start adding conditions to it, these will change the value of the Bayes factor, as we have already seen. So I have no problem acknowledging that eyewitness testimonies can often be mistaken, and that it's in human nature to give flawed testimonies under certain conditions. In such conditions the Bayes factor for a testimony must rightfully be severely discounted. However, one must also acknowledge that there are also conditions that dramatically enhance the value of human testimony - note the previous example of a chess game record, with a Bayes factor exceeding 1e120.
There is therefore bound to be a number of objections which effectively say "see how unreliable humans are (in these specific circumstances)!" What we must do, then, is to compare the circumstances in these objections to the actual circumstances surrounding the testimonies about the resurrection. We will see that, upon actually making this comparison, the testimonies for the resurrection are actually strengthened, rather than weakened, at nearly every turn by the specific circumstances surrounding them.
So, let's tackle the issue of eyewitness testimonies. The question of unreliable eyewitness testimonies typically come up in something like a courtroom setting, where a bystander is identifying someone they saw during an incident under investigation. A common example may have a policeman asking a witness, "now ma'am, can you point out which one of the fellows in that lineup was the one that pointed the gun at the cashier?"
Let's identify some of the common circumstances surrounding these events, about which such testimonies are made:
The witness is nearly always a bystander - a stranger who was previously not familiar with any of the actors in the crime.
The event in question often takes place in a matter of minutes, if not seconds. Witnesses are often caught by surprise - the crime takes place at its own pace, with no regard for making things easy for the witnesses. Indeed criminals often rely on the shock and the quick pace of the events to hinder possible identification and later prosecution.
There is often extreme stress placed upon the witnesses, who are fearing for their immediate personal safety. This may especially be the case if a weapon is present, which draws the focus of the victims or witnesses to it, and away from the proper identification of the perpetrator.
Related to the above, witnesses in such testimonies are often not primarily concerned with the identity of the perpetrator. In the moment, they are often simply shocked by the event, or mainly concerned about their bodily safety.
Now compare these to the testimonies about Jesus's resurrection:
Jesus was the most important person in the disciples' lives. He was explicitly more important to them than their family members or hometown friends. They had been around each other constantly for the last several years, and were familiar with one another as much as anyone can be.
Jesus's post-resurrection appearances occur multiple times, often in extended scenes where he converses with the disciples at length about what this all means. He eats with them, talks with them, and teaches them. Jesus furthermore specifically has these discussions for the benefit of the disciples, so that they can better understand his resurrection.
The pervasive mood during these post-resurrection appearances must have been awe and excitement. There is an optimal amount of stress for peak human performance, at a level which is neither too little (with accompanying boredom and lethargy) nor too much (with accompanying nervousness and panic). Speaking with the risen Christ must have put the disciples near this optimum peak, with an exhilarating atmosphere pervading every moment of their discussion.
The chief thought in the disciple's mind in each of these meetings must have been primarily about Jesus. 'Wow, it really is the Lord! He is risen from the dead! What could this all mean?' He commanded their wholehearted attention at each of these post-resurrection meetings.
So upon making this comparison, the result is clear. For each of the factors which causes courtroom eyewitness testimonies to be unreliable, the disciples' testimonies about Jesus are found to have the exact opposite property: they're testifying about someone they know very well (instead of a stranger), about events which happened repeatedly over an extended period of time (instead of being over in a flash), under the optimal amount of stimulation (rather than under crippling fear), with the person of Jesus as the chief object of their focus (rather than being shocked or focused on their immediate bodily safety). Insofar as the circumstances surrounding a typical courtroom eyewitness testimony cause them to unreliable, the same reasoning requires that the disciples' testimonies would then be especially reliable.
To put it simply, the example of unreliable courtroom witnesses only demonstrate how different the disciples' testimonies about the resurrection are. The disciples were not doing anything like saying "yes, that man with the red hair there is the man who pointed the gun at the cashier", with its accompanying uncertainty. No, their statement is rather more like a woman saying "yes, my husband really is the man I married at my wedding". Good luck finding many women who are mistaken about that.
Therefore, the Bayes factor associated with the resurrection testimonies must be greater than they were in the unconditioned case. 1e8 may have seemed like an overestimate upon a superficial comparison, but we've already seen that it is actually an underestimate: none of the factors that weaken a courtroom testimony are present, while all of their opposite qualities infuse the disciples' testimonies and correspondingly strengthen them.
Or actively deceptive?
Yet another class of objections may argue for 1e8 being too large, on the basis of people being intentionally deceptive rather than being mistaken. It may go like this:
"1e8 is a ridiculously large Bayes factor for people's testimonies. People lie all the time. Do you really think that only 1 out of 1e8 things that people say are lies? There are conspiracies, con artists, and fame seekers everywhere, at all times. What makes you think that the disciples reporting on the resurrection were not just one of these people?"
The objection here, and its answer, is much the same as before. Yes, people lie, or are otherwise unreliable, in some circumstances. These circumstances rightly require us to adjust the Bayes factor downwards. But the comparison of such circumstances with with what the disciples actually faced will only reveal their vast differences. If you think that people are likely to lie under certain circumstances, you must then therefore think that the disciples were highly likely to be truthful about the resurrection, due to the absence of these circumstances.
So, taking lottery winners again as an example: if someone claims to have won the lottery, their claim should be given about a 1e8 Bayes factor. But what if they then go on to say that they've left their winning ticket with a Nigerian prince, and that they would share their winnings with you if you would only give them $5,000 to cover their travel expenses to retrieve the ticket? Well, now the Bayes factor drops precipitously, down towards zero.
However, what if the supposed lottery winner instead gives lavish gifts to their friends and family, buys a new house, then hires a financial adviser to discuss the tax implications of their sudden windfall? Then the Bayes factor would dramatically increase, towards values like 1e120.
So then, what are the circumstances under which people are likely to lie? And in contrast, what are the circumstances that the disciples faced?
Well, people often lie for material gain, as in the above example of a con artist. The disciples, however, did not accrue wealth by claiming that Jesus had risen from the dead; in fact the very nature of their claim made this outcome highly unlikely, with the emphasis on serving the poor and a general disdain for worldly gain. If money was their goal, this was certainly the wrong way to go about it.
People may also lie under social, psychological, or physical pressure, as in the cases of false confessions obtained under harsh interrogation or torture. The disciples, however, resisted such pressure, and held on to their testimony under immense opposition of all kinds. The imminent possibility of persecution is a constant theme throughout the entire New Testament. In fact, many of the early Christian leaders underwent torture and martyrdom, including all three of the named witnesses I used in my calculation (James, Peter, Paul). We know how effective such treatment can be in eliciting false confessions even from their modern victims. We must therefore consider anyone who resisted the far harsher ancient versions of these treatments to be exceptionally trustworthy.
One may argue that at least the negative social pressure from society at large may be made up for by the approval from the close-knit Christian community. But this simply does not apply. Again, among the three named witnesses I used in my calculation, only one (Peter) was originally one of Jesus's disciples. James and the rest of Jesus's family are considered to have been in a somewhat disharmonious relationship with Jesus before the resurrection, and Paul was a complete outsider - an early persecutor of the church, whose personal and social identity was very much set in opposition to Christianity. So in a majority of these cases, the close-knit approval would have gone the other way: they would have ample reasons to reject the resurrection. Their testimonies in spite of this, therefore, must be counted as being much more reliable than the average.
People may also lie for fame - they claim to have achieved something remarkable or to be someone special. But as we have just seen, the fame that came with proclaiming the resurrection would have been exactly the wrong kind; the witnesses would have been shunned both by the Roman and Jewish society at large, and in many cases by their immediate social circle. Furthermore, it is the nature of fame to be fleeting; few would continue to lie for fame, in the face of intense opposition, for decades at a time, long after the shock of the initial claim wore off, to the point of death. Indeed, if the witnesses were fame-seekers of this type they would have done quite well by recanting the resurrection at the last minute and becoming a kind of whistle-blower for this deception that Christians pulled over the world. And yet, the witnesses did no such thing; they all died as martyrs.
People also sometimes lie for a cause. If they believe that some agenda is good and important, that may cause them to be deceptive "for the greater good", to advance that agenda. But this is impossible given the theology of the early church. Jesus was the greatest good; his resurrection was the most important event in the whole world. There was nothing greater which would be worth lying about the resurrection.
In all this, the actions of the witnesses were in perfect accord with their genuine belief in the resurrection. They had no reason to lie and every reason to tell the truth. We, also, have no reason to believe they were liars and every reason to believe that they were truthful.
So, it is true that men often lie. But this is a shallow observation. Upon considering the actual, specific circumstances surrounding the resurrection testimonies, we find that they are diametrically opposed to the circumstances conducive to lying. Therefore, the observation that "men often lie" only serves to enhance the trustworthiness of the witnesses to the resurrection, by pointing out how different these witnesses are from typical liars.
We ought to have reduced the Bayes factor for the resurrection testimonies down from 1e8 had we found the surrounding circumstances conducive to lying. But since the opposite has happened, we must therefore increase the Bayes factor. 1e8 is a distinct underestimate of its true value.
Or actually crazy?
Another class of objections would just argue that the witnesses to the resurrection were crazy:
"Obviously anyone who claims that they saw someone coming back from the dead is crazy. How can we take their stories about these outlandish miracles seriously? Clearly there was something mentally wrong with these people, and we ought to dismiss their 'testimonies' as the ramblings of the insane or the schizophrenic."
By now, it ought to be obvious that I'm going to handle this objection like all the others. Did the witnesses to the resurrection act like they were crazy? Did they exhibit the typical behaviors of the insane or the schizophrenic? If they did, we should rightly lower the Bayes factor for their testimonies from the relatively unconditioned value of 1e8. But if they did not, then by the same logic we must increase the Bayes factor.
This investigation is straightforward enough: read the New Testament, and look for symptoms of mental illness in areas that are not directly related to supernatural claims (one must be careful about circular reasoning). So, does the New Testament read like the work of a schizophrenic? Does it seem to describe people who were afflicted by mental illness? Would you say, for instance, that Peter's sermon at Pentecost exhibits problems with attention or memory, or that Paul's letter to the Romans demonstrate disorganized thinking?
In fact, apart from the supernatural components, I have not heard of anyone citing any part of the disciple's work in the New Testament as being characteristic of mental illness. If there is such a passage, I'd love to know about it. Can anyone point to a verse and say, "here is where Paul shows clear signs of psychosis", or "this is where Peter displays the classic symptoms of schizophrenia"? It says a great deal about the "insanity" accusation that the only evidence they can find for it are the very parts that make up the question at hand, the very parts they object to. In short, the objection effectively only amounts to saying "I disagree with these people on these points, so they must be crazy!"
On the other hand, there are plenty of reasons to think that the witnesses to the resurrection were of sound mind. Remember, they were the organizers and leaders in the early Christian church - a movement that spanned their known world. Furthermore, recall that they were successful beyond any naturally possible expectations: Christianity has lasted thousands of years until the present day, multiplied wildly, and now spans the whole globe. Can anyone give any example of an organization run by insane people that was even a millionth as successful?
In particular, the ideas behind this organization - that is, the theology of the early Church - are readily available to us as the text of the New Testament. They are the most read, discussed, studied, and applied texts to have ever been written. If you're reading this you're also free to go read the New Testament. Does it seem like the work of the insane? What other product of madness has ever reached a fraction of its stature?
So the conclusion is clear enough. Once again, upon actually considering the facts surrounding the resurrection witnesses, we find that they do not correspond at all to the scenario in the objection. The disciples display no sign of insanity, instead demonstrating many characteristics of sound and acute minds. So, according to the very logic embedded in the objection itself, this must again increase the Bayes factor of their testimonies. As we have repeatedly said, 1e8 is an underestimate. The true value must be higher - likely in excess of 1e9 - and this is borne out through the empirical, historical record.
Or some combination of the above, or something else entirely?
Here is another typical attempt to deny Christ's resurrection:
"It may be that some of the disciples were crazy or especially grief-stricken after Jesus's crucifixion. This lead them to see some vivid visions of Jesus, which they related to the other disciples. Some of these other disciples, who had not seen the visions themselves, then spread the story about the 'resurrection' based on the vision of these few crazy people. Then, a few other disciples, who were dissatisfied with Judaism, formed an opportunistic conspiracy to start a new religion based on these budding stories about this 'resurrection', and that's how Christianity started.
Or, it could have gone another way. A few disciples wanted to start a new religion and formed a conspiracy. After Jesus's death, they suggested to some of the other, more gullible and mentally unstable people that Jesus rose from the dead. With a little faking of evidence, social pressure, and the power of suggestion, they eventually got enough of the other disciples to say that they saw the resurrected Jesus themselves. From there, the resurrection became part of their faith narrative, and that's how Christianity might have started.
There are dozens of other possibilities like these - it doesn't have to be that everyone was lying or crazy. We just need the right combination of lies, mistakes, and insanity at the right times and situations for Christianity to start. Surely, it is more likely that one of the many possibilities represented here lead to the belief in the resurrection rather than for Jesus to have really come back from the dead."
We can, of course, answer this objection like we answered the previous ones: there is less than no reason to give credence to any of these scenarios, so the Bayes factor for the resurrection testimonies must therefore correspondingly increase. As the current objection is merely combinations of already discredited previous objections, this is quite adequate.
But there is a more pressing concern: anyone willing to entertain objections of this type has a fundamental misunderstanding of how Bayesian reasoning works. This has likely led them to vastly underestimate the strength, resilience, and robustness of the argument for the resurrection. Much of the above sections, about how a failed objection actually strengthens the case for the resurrection, was probably lost on them.
For these reasons, we now need to go over the nature and strengths of a Bayesian argument, and how it handles all such simplistic objections.
The nature of Bayesian arguments.
After hearing many objections in succession as we just have, it's easy to lose sight of the big picture. For instance, one may fall into the trap of thinking that if even one of these objections has even the slightest chance of being true, the argument would fall apart. But is that really the case? If the disciples had even the slightest chance of being crazy or mistaken or deceptive about the resurrection, would that cause the whole chain of reasoning to break and the case for the resurrection to collapse?
Bayesian arguments are not deductive arguments.
It's true that a standard deductive argument does work like that - A and B together lead to C, which lead to D, which then leads to the conclusion. For such an argument, all of its premises must be entirely true and each step of its reasoning must be completely correct. Anything else invalidates the whole argument. That is why a barrage of objections can sometimes succeed against such an argument, or at least cast doubt on its soundness.
But my argument for the resurrection is not a deductive argument. It is an order-of-magnitude probability estimation using Bayesian reasoning. The objections against it can only take two forms: you must either claim that I'm misusing the mathematical apparatus (that is, Bayes' rule), or disagree with my estimated probability values.
It is easy to fall back to thinking in terms of a deductive argument when you hear many frivolous objections in succession - that one of them must eventually get through a chink in the armor and deliver the fatal blow. If only someone could just be clever enough to think of that one silver bullet! But this simply does not apply to our case. Bayesian arguments are naturally and fundamentally immune to this type of attack.
Bayes factors do not require certainty.
The point here is that in the wrangling over probabilities need not produce absolute certainty. The argument does not depend on it. I do not need to claim, for example, that there is absolutely no chance that the disciples were lying. Having demonstrated that the Bayes factor for a typical, relatively unconditioned human testimony is around 1e8, I only need to demonstrate that the disciples are not more likely to be liars than such a "typical" person. In fact, anything which suggests that the disciples' honesty exceeded that of the "typical" person actually strengthens the argument beyond its original form, by increasing the Bayes factor. This is what has actually happened upon the examination of every objection thus far.
(new material) You do not get to choose to be not convinced.
Bayesian arguments are robust.
But let us imagine that one of these objections somehow actually succeeded. Say, for instance, we found actual evidence where the disciples were offered a monetary compensation from an external source for spreading stories about a resurrection. What would it do to the resurrection argument?
This would still not be a fatal blow. A single objection - even a completely real, legitimate, successful one - doesn't simply invalidate a Bayesian argument. We would merely have to re-calculate the final odds. In the above example, the scenario would correspond closely to the 9/11 fraudsters lying about their victimization, so the Bayes factor of the disciple's testimony would likely drop from about 1e8 to 1e6, according to our previous calculations.
But even with this theoretical coup for the skeptics, this would not materially change the outcome. As we have previously calculated, a Bayes factor of 1e6 still gives Peter and Paul's largely independent testimonies enough strength in combination to overcome the prior of 1e-11, and the remaining testimonies in 1 Corinthians still provide overwhelming evidence for the resurrection.
That is the robustness of a Bayesian argument, and the argument for the resurrection in particular. A few objections - even completely real, legitimate, and successful ones - are unlikely to do more than put small dents in it, while unsuccessful objections actually strengthen it.
Of course, this assumes that the objections are successful in the first place. And here, we get to the main problem with these previous simplistic objections, and the reason why all of them can be simply dismissed out of hand.
Only evidence moves the odds. Speculations do nothing.
Imagine, for instance, that your friend claims to have been struck by lightning. You've taken stock of this claim, and based on the empirical evidence of other similar claims, decided to assign it a Bayes factor of 1e8. But then someone says, "well, your friend may be just a little crazy. And he might have had a nightmare about a thunderstorm last night. Then he might have gone to a hypnotist who had him recall that nightmare, which he's now confusing with reality. Or maybe it was the hypnotist who planted the suggestion in his mind first and that caused his nightmare. Really, it might have been any of these things - and isn't it more likely that at least one of these possibilities is true, rather than for him to have been actually struck by lightning?"
Should you or your friend then discount the previously assigned Bayes factor in light of these new possibilities? Absolutely not. Again, the Bayes factor ALREADY includes all of the ways that this claim may be wrong. It is the numerical estimation of the weight of evidence for a human testimony, and as such already inherently includes the possibility that the evidence may be misleading.
Having established its value, it is simply incorrect to further modify it with no evidence, based on enumerating possibilities that were already included in its evaluation. Your friend's proper reply to this wild speculation would be to say, "what makes you think that I had visited a hypnotist or had a nightmare? Of course, anyone might be wrong about anything in any number of ways - but my friends already know how much trust to put in my testimony. How does a list of ways that I might be wrong, with no evidence behind any of it, make them trust me less?"
Now, is there any evidence that your friend did really visit a hypnotist recently? Then it is proper to include that evidence to re-calculate the probability of the lightning strike. Similarly, is there any evidence that a crazy group of Jesus's disciples reported on the resurrection, which then got hijacked by a conspiratorial group of disciples? Then it would be proper to include that evidence to re-calculate the probability of Christ's resurrection. However, in the absence of such evidence, the mere existence of that possibility cannot change our calculations. Such possibilities are already included in the initial calculation.
Of course not. In modifying your empirically calculated probability, you must only consider the evidence that you actually have. You must disregard any evidence that you could have had, or wish you had. So, in the absence of any evidence, the probability for 'heads' is still 0.5, and the innumerable ways that the coin might turn out to be 'tails' does nothing to change it. Now, it may be that you recorded the first part of the coin flip in slow motion, and it turns out that the coin did indeed strike the table at an angle of 15 degrees for its leading edge, with an angular velocity of 12 rev/s and a downward linear velocity of 2 m/s. That would be evidence. That would cause the probabilities to change. But the mere possibility of this happening, in the absence of the actual evidence, does not change the probability.
Here is the evidence that we actually have: numerous witnesses gave their earnest, personal testimonies, saying that they personally saw the risen Christ. We know how to numerically evaluate such evidence. We have already numerically taken into account the many ways that they may have been wrong, whether through honest mistakes, deception, or insanity. All such possibilities are already included in our Bayes factor of 1e8. We have less than no evidence that anything like the speculative scenarios in the objections have taken place, and the mere possibilities for these speculations cannot change the empirically derived probabilities. Therefore the odds for the resurrection remains undiminished by the objections: Jesus almost certainly rose from the dead.
The lack of evidence against the resurrection
In answering these objections, we've touched on the lack of evidence for giving them any consideration. A skeptical reader may wonder whether I've ignored any evidence against the resurrection, or how I would answer this or that argument by this or that person. A large part of my reply would be that there is no significant evidence against the resurrection.
Let me reiterate and clarify that, because it's important. There is an utter lack of evidence for disbelieving the resurrection: literally every single document we have by the people who were actually connected to the event to any reasonable degree ALL portray the resurrection as something that actually happened.
If you believe in the resurrection, you have the unanimous support of every author who were actually close to the event and would know for certain. If you disbelieve the resurrection, literally all such evidence - every single testimony of every single individual who ever wrote personally about the actual event - is against you.
So, I'm not being selective about the evidence. There is nothing to be selective about, because there is essentially no evidence for the opposing argument. This is why I'm fundamentally unconcerned about any arguments against the resurrection: because they have no evidence. The only thing I've done in choosing my evidence was to handicap my own argument, by only using a small fraction of the total evidence available.
If there were any evidence against the resurrection, I'd be glad to incorporate it into the calculation. I've already said elsewhere that a sufficiently strong evidence against the resurrection can falsify the whole hypothesis for me - if, you know, such a thing actually existed.
So, does anyone know of a cave in Israel that houses Jesus's mummified corpse? By all means, tell me about it. Is there an ancient manuscript that exposes the disciples' conspiracy to fake the resurrection? Let me know. Is there a record of a Roman interrogation where an apostle confesses to having made up the whole resurrection thing? Is there an epistle where a disgruntled disciple warns the others about staking the faith on a schizophrenic woman and her crazy resurrection story? Is there any record of a psychoactive plant in first century Jerusalem that causes vivid mass hallucinations about the recently deceased? Is there a complaint from Jesus's family about how his message has been hijacked by a bunch of lunatics and their crazy resurrection story?
You see, nothing remotely like any of the above actually exists. There is zero evidence for disbelieving the resurrection.
This is why every single skeptical attempt at explaining the resurrection relies entirely on ignoring the existing evidence, and making stuff up instead. They have no other options, because they have no evidence on their side. That's why the only thing they can do is to ignore the existing evidence, and make stuff up.
So, when they say that Jesus's resurrection was a myth that grew over time to be accepted as fact, they're ignoring the existing evidence that says that the resurrection was at the very core of Christianity from its inception, and making stuff up instead about how a myth might have eventually gained enough traction to be accepted as dogma.
When they say that Paul might have converted because he already had second thoughts about Judaism before encountering Jesus on the road to Damascus, they are ignoring the existing evidence in Paul's own testimony, and making stuff up instead about what they think went on inside Paul's head.
When they say that the early Christians didn't believe in a real, physical resurrection, they are ignoring the existing evidence that unanimously say that Jesus's body was missing from the tomb, and are instead making stuff up about what they think the early Christians really thought.
When they say that Jesus might not have really died, but only swooned, they're ignoring the existing evidence that clearly presents Jesus's death, and making stuff up instead about the combination of circumstances that might have allowed Jesus to survive a crucifixion.
When they say that the post-resurrection appearances were only visions or hallucinations, they're ignoring the existing evidence that unequivocally states the physical nature of Jesus's new body, and making stuff up instead about the disciples' mental conditions.
When they say that the gospel writers were only interested in the theological and literary dimensions of their story, and showed no concern for the truth, they're ignoring the existing evidence from these writers themselves that directly contradicts them, and making stuff up about the writer's "true" motivations instead.
So, let's not be distracted by such made-up speculations. Remember the outline of the argument at hand. We are using Bayesian reasoning. We start with a prior odds for the resurrection, and modify it according to the Bayes factor of the evidence. Only evidence moves the odds; speculations do nothing. So we only consider the the evidence that we actually have, disregarding any wishful, speculative "evidence" we may dream up. Our calculation already account for any point the skeptic may want to make: the inherently unlikely nature of the resurrection is already included in the prior, and the possibilities for the disciples being wrong are included in the Bayes factors. Upon carrying out this calculation, using very conservative values, we find that the evidence completely overwhelms the prior. Jesus almost certainly rose from the dead.
The next steps
We've just discussed how there is no evidence against the resurrection: literally every single written record we have by the people who were actually connected to the event to any reasonable degree all portray the resurrection as something that actually happened.
However, it's worth asking - what's the closest thing to an 'evidence against the resurrection'? Are there any historical record from around the time of the event which suggests that the resurrection didn't happen?
Ironically, the closest thing I know is actually in the Gospel of Matthew, where the author mentions the guards to Jesus's tomb being paid off to spread a rumor about the disciples stealing the body. So, I suppose at least some people at the time were saying that Jesus didn't really rise from the dead.
Now, this hardly count for anything in terms an opposing evidence - we don't have an actual personal testimony, our source Matthew clearly presents it as a lie, and if anything it confirms that the tomb was guarded and yet turned out empty.
However, it is instructive to see the nature of this lie. Why did they choose this lie? What do people do when they're faced against a mountain of evidence against their position, yet must find ways to ignore that evidence? What do they do when they know they're wrong? They turn to a crackpot theories, of course. They do things like make up a conspiracy theory about the disciples stealing the body.
You see, we can now be very confident that Jesus rose from the dead. The calculation which first gave us this confidence has now been verified in multiple ways, using completely different methodologies, with everything solidly grounded in empirical, historical data. Everything checks out, and all the numbers are in harmony.
But all this has been computed under the assumption that there isn't any extreme dependence in the disciple's testimonies. We have not yet accounted for the possibility that the entire set of testimony about Jesus's resurrection might have been been engineered to be in agreement by some unknown force. That is to say, we've been discounting crackpot theories - like a conspiracy by the disciples to steal Jesus's body, or an alien mind-controlling all the witnesses to the resurrection.
Note that this is beyond any kind of "normal" dependence, like ordinary social pressure or group conformity. The case for the resurrection is so strong that even when such mechanisms are included the conclusion is beyond doubt: recall that even just Peter and Paul's testimonies, with full dependence factors, was enough to safely conclude that the resurrection happened. No, the kind of crackpot theory we're talking about would involve, at a minimum, a conspiracy involving the disciples and their enemy Paul, and a plan to persecute their fellow Christians, offend their fellow Jews, and invite the ire of Rome, all for no discernible gain.
Ignoring such theories is fine and good, as long as both sides of the debate are agreed in dismissing them. Most doubters of the resurrection do not subscribe to these extreme theories, so carrying out our calculations in this way up to this point was still productive. However, they're now facing an overwhelming amount of evidence. Even a small fraction of it possesses a Bayes factor well in excess of 1e11. The total Bayes factor, without crackpot theories, turned out to be something like 1e48, even with some 'ordinary' dependence factors included. The final odds turned out to be something like 1e37. All the key steps in the argument have been double-checked and re-verified in multiple ways. The posterior probability against the resurrection has now become so tiny, that the small prior assigned to crackpot theories now seem much larger in comparison. Someone set on disbelief can no longer ignore these theories. Indeed they have no other choice: they must fully embrace these crackpot theories.
Examining crackpot theories, in general
Let us examine this general class of theories, that postulate a near-total interdependence in the evidence against them. What kind of theories are they? What are their properties? Is it fair to characterize them as "crackpot" theories?
Now, note that such theories generally require a conspiracy of some kind, almost by definition. Near-total interdependence means that what appeared to be many pieces of evidence was really just controlled by a singular false entity, which manufactured all the other pieces of evidence. Whether this source was a group of disciples or an elite Roman secret society or some space aliens or whatnot doesn't particularly matter - All such theories share the following traits.
The first thing to note about such theories is that they have very low priors probabilities to begin with. Indeed, among those skeptical of Christ's resurrection, a theory of this type is almost never their first choice. Few people want to be labeled a conspiracy theorist, after all. The skeptics want the resurrection testimonies to have been produced "naturally". They'll invoke known social phenomena such as myth generation over a long time, or religious fervor or delusion. They want such ordinary explanations to be a plausible way to generate the resurrection testimonies. Of course, what we've demonstrated thus far is that such explanations are in fact not plausible.
Maybe some people will say that they'd rather be a conspiracy theorist than believe in the resurrection. But even so, such people only say this as a backup, while still trying to argue for a more ordinary explanation.
So, conspiracy theories and other similar hypothesis have low prior odds, even in the mind of skeptics. This is appropriate, as conspiracies are in fact very rare.
Secondly, these 'near-total interdependence of evidence' theories are designed to ignore the evidence. They are chosen precisely because they allow their adherents to say "but that's exactly what they want you to think!" to any evidence you bring against them. It's important to note that this is not an accidental, fortuitous property of these theories. 'Near-total interdependence of evidence' is the defining feature of such theories, and it's precisely that feature which allows them to dismiss all the evidence which would weigh against more likely theories.
In combination, the above two facts mean that such theories cannot really hope to win the day. Since they start with a low prior, and are designed for ignoring the evidence, they cannot really hope to prevail - they need evidence to increase that low prior odds, but they're designed mostly to ignore evidence.
Note that, when a conspiracy theorist ignores evidence by saying "that's exactly what they want you to think!", this doesn't actually help the theory. It merely softens the impact of that evidence. Yes, the conspiracy theory has "explained" the evidence, but only about as well as the rival theory. The Bayes factor therefore stays around 1, meaning nothing has changed on that front, and the probability for the conspiracy theory remains at its low prior value.
But the conspiracy theory isn't totally immune to such evidence, because the prior probability itself now becomes a lower value. A greater conspiracy that explains more - one that is more vast and has planted more evidence and covered it up better - is a priori less likely to have come about than a lesser conspiracy. So a piece of evidence dismissed by the conspiracy does still hurt the theory. The hope of the conspiracy theorist is that this harm in the prior odds will be less than the exponential rate of harm that a fully independent piece of evidence would normally cause.
So the most such a theory can realistically hope for is a kind of non-total loss, where they lose less quickly and hope to say "at least it's not impossible!" at the end.
Now, there are very particular kinds of evidence that does help them - the ones that specifically demonstrates a conspiracy. Something like a document from a secret meeting that lays out the nefarious master plan would work. But, of course, for a vast majority of these theories, such evidence does not exist.
So, given all these traits - given that they are highly unlikely theories that are designed to ignore the evidence, with little chance at any positive evidence for them - I think it's fair to call them crackpot theories.
Yet some people will bring up even such theories. So we, too, must now consider them, and show that our conclusion holds firm even then.
Using the historical data to construct the skeptic's distribution
How can we quantitatively tackle things like conspiracy theories? What do we do about the interdependency of evidence? One can already imagine the objections to any such attempt. Every assumption would be questioned, and every ridiculous possibility brought up demanding a full numerical treatment. Even if a traditional conspiracy were to be fully debunked in a numerical argument, a skeptic would just weasel the argument to be about a "groupthink induced by religious fervor" instead, and when that got debunked, they would just say "but what about aliens?" Indeed, such weaseling is often the point of bringing up things like conspiracy theories in the first place: not to actually advocate for them, but to make the calculation appear intractable.
But I did title this part "addressing all possible alternatives" - and that's exactly what I'm going to do. My argument will take EVERYTHING into account - government conspiracies, religious groupthink, practical jokes by aliens, everything. Furthermore, my approach will be fully quantitative. Every single possibility for every conceivable degree of evidence dependence will be fully considered.
In addition, empirical evidence will be the foundation of my whole argument. That is, in fact, the key that makes it totally comprehensive. Do you remember the following graph?

That is the level of empirical evidence that history has actually recorded for the resurrection of various individuals. It's a partial histogram - note the differing number of people with different amounts of evidence for their resurrection. This suggests a probability distribution.
If we exclude Jesus and the other Christian resurrection reports, the probability distribution we get would be the exact model that an empirical skeptic of Christianity must use, in predicting the likelihood of a resurrection report. Essentially, the idea is that we can calculate the probability of getting a certain level of evidence for a resurrection, based on how frequently similar reports have come up in history.
Note that, because the raw data is gathered from empirical reports collected in history, this automatically accounts for things like conspiracy theories. The possible interdependency of the evidence is fully included in this model. So you think that a great deal of evidence can be built up through a conspiracy, because the evidence doesn't have to be independent? The distribution includes all such evidence-manufacturing conspiracies that actually existed in history. You want to switch your argument to a religious mass delusion instead? The result of all such mass delusions are also included, at the level of evidence that they actually generated in history.
How about something that has probably never happened in history at all, like some aliens faking a resurrection as a joke? Even these possibilities are included, through at least two mechanisms. For one, there are a great many multitude of such unlikely scenarios - and at least one of them might have actually occurred in history, even if any specific one of them was unlikely. So we would have a record of such evidence in aggregate. And secondly, even if such unlikely scenarios never occurred, they can still be accounted for in the modeling of the probability distribution from the samples we actually have. As an analogy, if you were to model people's heights by sampling a thousand people, you can still deduce that human heights follow a roughly normal distribution, and can thereby figure out that there would be someone out there who's at least 7 feet tall, even if such a person was not in your sample.
So you see, this method does in fact take everything into account. It does generate the exact model that an empirical skeptic of Christianity must use. That's the great thing about arguing from empirical, historical records. You can bypass all the difficult and controversial calculations about the probabilities of conspiracies, or the precise degree of dependence among the evidence. All of that automatically gets incorporated into the historical data at their actually correct historical values, and all we have to do is to read off the final result. So a skeptic cannot reject this probability distribution without rejecting history or empiricism.
Once we understand this "skeptic's distribution", the rest of the calculation is fairly straightforward. We use the distribution to get the "skeptic's probability" - the likelihood of naturalistically generating a level of evidence matching Jesus's resurrection reports. We then repeat the same thing for the Christian's position, that Jesus really rose from the dead: we obtain the "Christian's distribution" and use it to calculate a "Christian's probability". The Bayes factor is then simply the ratio of these two probabilities of the two competing hypotheses. Lastly, we apply the Bayes factor to the prior odds, to see if it's enough to overcome the low prior for the resurrection.
Assigning numerical x values
This approach of comparing the two distributions needs to be fully empirical and quantitative. This in turn requires a precise definition of the x-axis values in the above graph. The axis as been labeled "Amount of evidence", but what does that mean exactly?
To pin down this definition, let's start by fixing one point on the axis: the one labeled "'once in non-Christian world history' level". This is the amount of evidence associated with the single most convincing non-Christian resurrection report in world history. It is the level of evidence such that it narrows the field down to exactly one. We will assign this fixed point the value of x = 1.
Note that this is a fully empirical and quantitative way of fixing this point. Given the record of history, we can always raise the bar of required evidence until all but one non-Christian resurrection report is eliminated, and this report then becomes our fixed point that defines x = 1, the single most convincing non-Christian resurrection claim in world history.
Once we have this idea, assigning other x values is easy. Values of x greater than this point are obtained by simply multiplying by the number of claims. If one such "once in world history" claim has an x value of 1, two such claims in agreement about the same resurrection would have an x value of 2, three would have 3, and so on. Of course, we would not see x = 2 or 3 within non-Christian world history, since the highest value there is x = 1 by definition. But we would know where to place them if we observed such claims in Christianity.
Then the level of evidence for Jesus's resurrection would, at a minimum, be placed at x = 6, for each of the six pieces of evidence in 1 Corinthians 15 was individually greater than x = 1: none of them could be matched by anything else in non-Christian world history. In fact, none of them even had anything remotely close to approaching them. This tells us that they should actually be placed at x values significantly greater than 1, since at x = 1 one would still expect that multiple other cases would be somewhat comparable to them.
Here's an example: consider the statement, "I saw grandma in my dreams after she passed away - so that's evidence for her resurrection". Now, this is clearly a very weak piece of evidence. On no account should you believe that someone came back from the dead just because you dreamt about them. Lots of people have dreams like this after a loved one passes away. But how can we quantify just how weak this evidence is? Where exactly can we place this on our x-axis?
The key is in the fact that "lots of people have dreams like this". In fact, so many people had such dreams that they may even have had them about the same dead individual. Consider all the reportable deaths throughout non-Christian world history. Of those 1e9 deaths, which one had the largest number of people report a dream about the deceased afterwards?
Let's say for the sake of this example that this highest dream-count occurs for someone who died and had 100 people report a dream about them afterwards, and that this make them the most convincing non-Christian resurrection report in world history. Because this is the unique, best, "once in non-Christian world history" piece of evidence which narrows the field down to only itself, it would be the fixed point at x = 1.
In addition, this establishes the relationship between any one dreams and our x axis: here, 100 dreams equals x = 1. This means that a single dream can be placed at a x value of 0.01. This corresponds to a very weak piece of evidence hardly worth mentioning, just as we said.
Note that there is nothing in our x-axis that enforces dependence or independence. There is no direct transformation between Bayes factors and our x values. All of these will be taken care of by modeling the skeptic's and Christian's distributions individually. The Bayes factor will be determined by the type, shape, and ultimately the exact values of these distributions at certain x values.
What should be the form of this "skeptic's distribution"?
How about we fit the "skeptic's distribution" to a normal distribution? Well, that would be plainly ridiculous. Even with very conservative estimates, the data we have gives the level of evidence for Jesus's resurrection at x = 6. Our goal is to get the probability of something like this happening.
But if we used a normal distribution for the "skeptic's distribution", this could essentially never happen. Recall that human heights roughly follow a normal distribution. Then, our problem would be analogous to looking for someone 6 times taller than anyone else in history - that is, someone well over 50 feet tall. The chances for that is essentially zero. So if we chose the normal distribution, we'd essentially be dooming the skeptic's case from the start.
The same is true for an exponential distribution. An exponential distribution decreases in its probability value by a constant factor for each unit of increase in its domain. As the domain for our problem is "amount of evidence", this means that each piece of evidence would multiply the probability values. That is to say, we'd be treating each piece of evidence independently. So this effectively amounts to ignoring dependence factors, and we've already seen that this leads to numbers like 1e54 for the Bayes factor, again dooming the skeptic's case from the start.
This is a testament to how quickly these distributions decay as they extend to the right. Their right tails are so "stubby" that the maximum values of their samples are strongly restricted, and getting something 6 times greater than that maximum is essentially impossible. Picking any such distribution would not be fair to the skeptic's case.
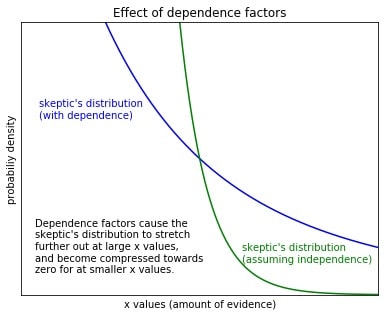
In fact, we can roughly sketch out the shape of the distribution based on the requirements of dependence. Dependency of evidence means that latter pieces of evidence have an easier, more likely chance of being generated, even if they're false. The skeptic's distribution would represent this by having larger probability density at larger x-values. Of course, this probability needs to come from the only places where it could: at the smaller x-values. Overall, you can kind of think of this as an warping of the exponential distribution which represents independence: at large x values, the probability distribution gets stretched out towards even higher x values, but since the overall distribution must be normalized, this extra probability must be taken away from the smaller x-values, which means that the distribution must get compressed towards zero at the smaller x values.
This is a description of a distribution with a "long tail" - something that has a chance for a new high record to beat the previous record by factors like 6. Something that decays slowly enough that its probability values remain non-negligible as we move further to the right. The distribution should still be realistic and have some justification for being selected, but we want to give the skeptic the best chance.
Taking all that into account, I have chosen a power law function for the form of the "skeptic's distribution". This should not be a surprise - indeed anyone familiar with the statistics of human behavior might have guessed it from just the previous graph of the histogram we're trying to fit.
There exists distributions that decay even more slowly than a power law, but they're rare, obscure, and have no relation to what we're doing. By contrast, power law distributions are ubiquitous in human behavior. They form the basis for the well-known Pareto principle, and they aptly capture the "dependency of evidence" factor we're currently trying to model.
For example, the distribution of income among people follows a power law. A few people, out at the long tail, have a great deal of wealth, because rich get richer - that is, because how rich you get depends on how rich you already are.
The size of cities also follows a power law. There are a few very large cities out at the long tail, because your chances of moving to a city depends on the number of people who already live there.
The number of links to a website follows a power law. There are a few, very popular websites out at the long tail, which have a lot of links to them. This is because a site's chances of getting a link depends on its popularity - that is, on the number of links it already has.
Don't let the specificity of these examples fool you. There are many, many more. Power law distributions are, as I said, ubiquitous in human behavior. They will frequently come up when one human behavior depends on the same kind of behavior, either by others or by the same person. In the current context of things like extreme dependence factors, this is because the chances of generating an additional piece of evidence for a resurrection depends on how much evidence it already has.
So there are excellent reasons to expect that the "skeptic's distribution" will follow a power law. It is entirely appropriate that we model it this way. Power laws accurately model dependence factors, as demonstrated by many well-known examples. They also give one of the best possible chances for the skeptic's case, having a very "long tail" and allowing for a "black swan" event like the level of evidence in Jesus's resurrection event.
Details of the distribution: generalized Pareto distribution and its parameters
So we've decided on a power law as the general form of the "skeptic's distribution".
The details of the distribution near zero will not particularly matter. We're more concerned about how rapidly it decays at very large values. This allows us quite a bit of leeway in choosing the specific form of the power law distribution, as they all decay similarly as we move along the tail off to the right.
For this reason, I've chosen the generalized Pareto distribution as the specific form of the "skeptic's distribution", guided chiefly by the straightforward interpretation of its parameters. But the choice here will not affect any conclusions. Any other power law distribution would give nearly identical results.
The generalized Pareto distribution is characterized by three parameters: location, scale, and shape. The location parameter determines where the distribution starts. It's where the probability density of the distribution is the largest. As the vast majority of humans have zero evidence of having risen from the dead, the location parameter should obviously be set at zero.
The scale parameter is irrelevant; it only controls the linear scaling of the x-axis of the distribution, and it can be arbitrary changed by changing the unit of evidence we use. As we've discussed previously, we've fix the scale so that a "once in non-Christian world history" has a fixed x-value of 1, and everything else is scaled from that. This determines our scale parameter.
The shape parameter is the interesting one. It's what we really care about. It effectively determines the power in the power law, and controls how quickly the function decays as the amount of evidence increases, and ultimately determines whether we can get a Jesus-level resurrection report out of a non-Christian world history.
For example, this is what the tail end of the distribution looks like with various shape parameters:
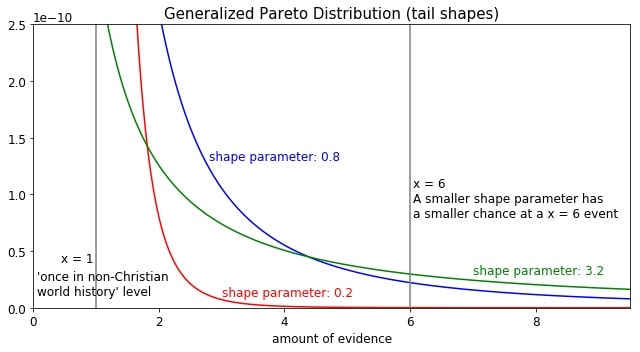
In each case, the distribution has been scaled so that the total probability to the right of the grey line at x = 1 is 1e-9. So the area under the curve for x > 1 is the same for all the colors, and x = 1 is where you'd expect the maximum value out of 1e9 samples to appear. As we said, it's the level of evidence corresponding to a 'once in non-Christian world history' level.
However, with the shape parameter at 0.8 (blue curve), we see that the decay rate is much slower, and there is some amount of probability even out at x = 6. If this were the "skeptic's distribution", it might have a shot at generating a Jesus-level of evidence for a resurrection, even if that level were 6 times higher than anything else observed in non-Christian history.
A shape parameter of 3.2 (green curve) decays more slowly still. We can see that it comes in lower, and extends out further to the right. It's hardly decaying at all by the time it reaches x = 6 - it's nearly flat out there. In fact, it decays so slowly that if this were the "skeptic's distribution", it would have a non-negligible chance of generating an event at x values of much higher than 6, and even a Jesus-level of evidence may not be all that remarkable.
But how should we determine the value of this shape parameter?
Well, what kind of data do we have to determine the shape parameter?
We have the historical data, of course. We have some number of people who are said to have been resurrected in some sense, and each of these people have some amount of evidence associated with their resurrection claim.
The idea here is to "fit" these evidence data into a generalized Pareto distribution, and read off the shape parameter. However, this will be somewhat tricky. We do not have the complete data for all 1e9 reportable deaths throughout human history. We can reasonably assume that the vast majority of them would have essentially zero evidence for a resurrection, but the complete data set would be pretty much impossible to obtain. We don't even have the complete data set just for the "outliers" - cases like Apollonius or Zalmoxis, where there is a distinctly non-zero level of evidence for a resurrection. Furthermore, the precision on determining the level of evidence is rather poor. All this means that the usual "fit a curve through some kind of x-y scatterplot" approach would not work very well.
However, given that we already know we'll be fitting a generalized Pareto distribution, this type of curve-fitting is not necessary. We're just looking for the shape parameter, and for that, we merely need to count the number of "outliers", which approach near the maximum value. Consider the following graph:
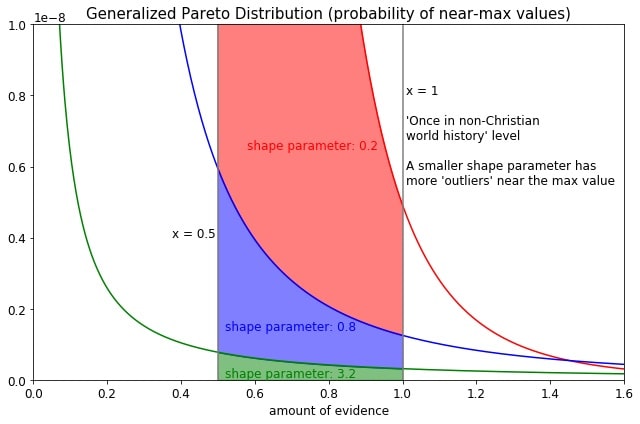
This is the same graph as before, in the sense that it just shows the generalized Pareto distribution, scaled so that the probability of x > 1 is 1e-9. Once again, this means that the maximum evidence from 1e9 reportable deaths is likely to appear around x = 1, at the "once in non-Christian world history" level.
However, we now want to focus on how to fit the data. And since the data will have x values less than the maximum, this particular graph is focused on the left side of the x = 1 line, instead of the tail to the right.
In particular, note the large differences in the area under the curve for different shape parameters. The shaded regions represent the probability of finding an "outlier", which would be a figure like Puhua or Aristeas. This difference in "outlier" probabilities can be used to determine the shape parameters.
Defining "outliers"
If we're going to use the concept of "outliers" in determining the shape parameter, we'd better be careful in its definition.
We already have several stories of non-Christian resurrections, of figures whom we've mentioned several times already - Apollonius, Krishna, Horus, and so on. These are among the class of people with the greatest amount of evidence for their "resurrection". They appear regularly in "see-Jesus-wasn't-special" lists compiled by non-Christians.
A common feature of these stories is that the evidence for their resurrection is rather weak. It's what I've referred to as the "some people say..." level of evidence. But let's define this level of evidence more carefully, so that we can place these people more firmly on the x-axis of our graph, as "outliers".
The "some people say..." level of evidence is assigned to a claim when it is sustained through multiple generations in a group of people by relying chiefly on the dependency factor of human testimony, in the absence of historical, individual testimonies or other forms of empirical evidence. It's essentially what gets passed on and down because "that's what people say", and for no better reason. So, specific, detailed myths are excellent candidates here, as are other localized superstitions.
Where can we place this kind of resurrection stories on the aforementioned x-axis? Well, since they exist, they must be at or below the singularly maximal actualized value, which is defined as x = 1. In fact they'd probably appear quite a bit below x = 1, since it's not clear that there is a singular non-Christian resurrection story with definitively the greatest amount of evidence behind it. Instead there seems to be several contenders for the "greatest evidence" slot, which means that they all fall short of it. But let's just ignore that for now. So, strictly speaking, they have an upper bound of x = 1.
On the other end, they must be placed above x = 0.5. This makes some amount of intuitive sense - after all, as weak it is, the "some people say..." level isn't all that weak. It's strong enough that there's only a relatively small number of them throughout history. If you, as an individual, tried to manufacture one, you'd probably fail. It's definitely stronger than, say, our earlier example of having a dream about your dead grandmother.
In fact, this relative rarity is again what allows us to assign it a lower bound. Recall what x = 0.5 means, by definition: it's the level of evidence which is sufficiently weak and common that a doubling up of that level of evidence, on an individual case, has been actually achieved once in non-Christian world history.
This is impossible for the "some people say..." stories, again by definition. Recall that an integral part of "some people say..." stories is that it's propagated chiefly through dependency of other people telling the same stories. If we doubled up two such stories - that is, if two different people groups told the same specific story about one specific individual rising from the dead - we'd suspect some kind of common influence which caused the story to be transmitted from one to the other. In other words, these "two" instances would really be the same instance, because the story was transmitted from one to the other, presumably through dependency of some storytellers. So such "doubling up" is nearly impossible, and we can simply eliminate stories at or below that level if we actually happen to find a case of it. This places the lower bound on the x-value of our "some people say..." stories at 0.5.
So that's our definition of "outliers": they are non-Christian resurrection testimonies in world history which would fall between the values of x = 0.5 to 1. This captures all of all instances of the "some people say..." resurrection stories we mentioned earlier, like Puhua or Dionysus.
Back to determining the shape parameter
Now let's look at the green curve in the previous graph, with a shape parameter of 3.2, and a tiny area under the curve. Just eyeballing it, the green area under the curve looks like it may be around 0.5e-9. So if this were the skeptic's distribution, you'd expect essentially no other outliers out of 1e9 samples, or perhaps one. The area under the curve is too small for much more. The maximum value would probably stand by itself, with few other outliers coming anywhere near its value.
Similarly, if the shape parameter is 0.8, the area under the curve is larger, and you'd expect more outliers. In fact, I'd eyeball the area under the blue curve as roughly 2e-9, so you'd expect perhaps two outlier out of 1e9 samples.
Lastly, if the shape parameter is 0.2, you'd expect many, many outliers. The probability distribution grows very rapidly as it goes backward from x = 1, and therefore you expect to find many other resurrection reports with a similar level of evidence as the maximum.
So by counting the number of outliers, we can make a determination about the shape parameters.
But... wait a minute. So having more outliers is associated with smaller shape parameters? But didn't smaller shape parameters correspond to a faster-decaying function, and therefore a lower probability for the "skeptic's distribution" generating a Jesus-level of evidence? Wouldn't this lead to the "skeptic's distribution" being less able to explain the evidence for Jesus's resurrection, and therefore make the resurrection more likely?
Are we saying that having MORE non-Christian resurrections reports make Jesus's resurrection MORE likely?
That is precisely what we are saying.
More non-Christian resurrections reports make Jesus's resurrection more likely
One simple way to see that is just from the above graph - the more probability there is with x < 1, the less there must be at higher values of x, like x = 6. This means that the "skeptic's distribution" is less able to explain an event with x = 6, so Christ's resurrection becomes more likely.
The following analogy may help understand this in a more intuitive way.
Alice accuses Bob of theft. Bob is known to have come into a sudden possession of $30,000. He is also known to be a gambler. He claims that his sudden fortune came from a lucky night of games of chance, but Alice believes that he stole the money - she claims that $30,000 is far too large a sum for Bob to have naturally won through gambling.
Carol takes on this investigation. She looks into Bob's past gambling history, to see if it's realistic for him to have won $30,000 in a single night. She finds that, among Bob's past verifiable winnings, there were two nights where he won $5,000 and $3,000. These are his most remarkable winnings on record, and Carol cannot find any other instances where he won more than $1,000 on a single night.
Carol concludes that she does not really have enough information. It could be that Bob plays a card game with an erratic payout scheme, where winning many times more money is not that unusual. Maybe it has some kind of "let it ride" or "double or nothing" mechanism which makes such returns plausible. Or maybe Bob himself is an erratic gambler, and decided to bet a lot more money than usual on the night when he supposedly won $30,000. Based on all this, Carol decides to be skeptical of Alice's claim that Bob stole the money. Her own "skeptic's distribution" for how much money Bob can win does not decay quickly enough. There are relatively few outliers near his maximum winnings of $5,000, and this suggests that it decays very slowly - meaning that the $5,000 cannot be established as a limit to what Bob can win. His theoretical winnings might possibly stretch out quite far into the higher values, making it impossible to rule out a $30,000 winning.
But then, Carol has a breakthrough in her investigation. She finds extensive, previously undiscovered records of Bob's gambling winnings, and it shows that Bob has won more than a $2,500 on dozens of nights. The maximum that he's won is still $5,000, but he's also regularly won thousands of dollars in a single night.
Carol takes this new information into account, and adjust her "skeptic's distribution" for how much Bob can win in a single night. Clearly, Bob's winnings are not erratic; he regularly wins up to about $5,000. But this also establishes, with the weight of those repeated winnings, that this is close to the likely upper limit for what he can win in one night.
Carol therefore decides to believe Alice. Her "skeptic's distribution" cannot explain how Bob would naturally win $30,000 in a single night, because it goes against his established pattern of regularly winning up to $5,000 as his maximum. She pursues the case further, and eventually convicts Bob of theft.
So, having more non-Christian reports of a resurrection, with their pathetically low levels of evidence behind them, only make Jesus's resurrection more likely. When skeptics say "don't you know there are numerous other Jesus-like stories of someone dying and resurrecting?", they are only kicking against the goads. The more such cases they come up with, the more firmly it establishes that Jesus really did rise from the dead.
The alternate hypothesis and its distribution
Bayes' theorem is essentially about comparing how well the competing hypotheses explain the data. As for the "no resurrection" hypothesis, we've already discussed the "skeptic's distribution" at length, to the point where we can almost specify it algorithmically. Now, we need to specify the "Christian's distribution" to the same degree.
By definition, the "Christian's distribution" assumes that Jesus actually rose from the dead, and asks how much evidence would be generated from such an event. It is thus a probability distribution function over the same x-axis that we've hitherto discussed. Once we have this distribution, the Bayes factor would simply be the ratio of the two distribution values at the actual level of evidence for Jesus's resurrection - say, at x = 6.
So, if Jesus really did rise from the dead, how much evidence could you expect for it? Certainly, it's not impossible (nothing ever is in Bayesian thinking) for even a real resurrection to leave no evidence. Jesus might have just quietly ascended to heaven immediately after rising from the dead, and nobody might ever know. This scenario may not be likely, but it can't be ruled out. But then again, it's also impossible to rule out the scenario where he shows himself to just one of his disciples, or to just two, or just to the twelve. Or, he could have shown himself to a full audience of Roman politicians and historians at the Circus Maximus, announced himself in a thundering voice, and ascended to heaven there. None of these could be definitively ruled out, because these are all only counterfactual scenarios. The only one of these which might not be counterfactual is the evidence that we actually have, the one that's summarized in 1 Corinthians 15. But, of course, we are not allowed to use the evidence itself to inform our likelihood.
But making note of all this allows us to begin shaping the "Christian's distribution". What should it look like? We know that it should be broadly distributed, and relatively smooth with no pronounced features. This reflects our ignorance: as we just said, we have no strong reason to prefer one evidence-generating scenario over another, so we treat them more or less equally, so our "Christian's distribution" should have no pronounced peaks or valleys.
We also know that our distribution can't go on off to infinity at a constant value, because it has to be normalizable. So despite its broad, featureless smoothness, it must have relatively more probability values at smaller x values. This would then decay slowly as you got to larger x values, off to infinity.
We can also ask what a plausible scenario would look like. I think we can intuit that scenarios like "quiet ascension with nobody knowing" or "full audience at Circus Maximus" scenarios are somehow unlikely. In fact, given that an itinerant preacher from some backwater parts of the Roman empire really rose from the dead, I think it's plausible that the evidence for it would include a number of witnesses who were personally and professionally close to him, and maybe some people who were in the crowds in some post-resurrection public appearances. A witness who was an hard-core skeptic in the beginning would be a nice bonus. That is to say, the actual amount of evidence summarized in 1 Corinthians 15 is quite plausible. This will help us set the "scale factor" for the x values.
But we must be vigilant against using the evidence itself to compute the likelihood. Furthermore, as before, we want to grant the skeptic every realistic advantage. This requires that we try to minimize the value of the Christian's distribution around x = 6. So we will not use anything of the "plausibility" argument above, except to hold it back as an additional margin of safety for our final conclusion.
So how can we minimize the Christian's distribution around x = 6? The silliest and most ad-hoc way would be to postulate a sudden dip in the distribution in that region - which would immediately violate our earlier requirements, that we know the distribution to be relatively smooth, with no pronounced dips or spikes. We can dismiss this "sudden dip" idea.
A second way would be to try to shove all the probability density to the smaller x values, so that by the time the Christian's distribution reaches values around x = 6 it would have decayed to nearly nothing. Essentially, the skeptic would be arguing that there's too much evidence for Christ's resurrection, and that it's unrealistic for there to be so much. But obviously, this is also pretty silly. You would have to somehow know, with a good deal of certainty, that the 1 Corinthians 15 scenario was excessive. You'd essentially be postulating a fairly sudden dip in the distribution somewhere below x = 6, with all its associated problems. We can safely dismiss this as well.
So the last and the most popular way to diminish the Christian's distribution around x = 6 is to argue that there should have been more evidence - way more evidence. So the skeptic will argue that the "full audience in the Circus Maximus" scenario is in fact too little, or that Jesus should have just stuck around on Earth and lived forever so that he can continually bear witness to his own resurrection. The aim is to stretch out the Christian's distribution to ever-larger x values, so that the likelihood at x = 6 gets diluted to nothing.
Now, there is certainly something to be said for this approach. It does somewhat fit the general shape of the Christian's distribution that we outlined earlier, which is broad, smooth, and stretches out to infinity. There are certainly more x values at x > 6 than at x < 6, so that's also something.
But it also has a number of problems. For one, we know that the Christian's distribution, despite its featureless broadness, must decay. This is true of all proper probability distributions, which are required to be normalizable. So we cannot expect the argument for larger x values to continue on to infinity with equal force. To do so would be allowing for the perpetual moving of the goalposts. Imagine if you did that in a murder trial: "I have a witness who saw the deed." "Well, why don't you have two witnesses?" "I do in fact have a second witness." "Well why isn't there a third?" So on and so forth. Since the skeptic could always demand additional evidence regardless of how much evidence actually exists, allowing for this line of argument indefinitely would mean that the null hypothesis must always be true in all inquiries.
So, that's the tension in the problem: we know that the Christian's distribution should extend far to the right, to larger x values, but we also know that it must decay, and therefore be constrained to be concentrated at smaller x values. The exact balance in this tension will determine the exact values in the Christian's distribution. But how could we find this balance?
As ever, we turn to the empirical, historical record.
Empirical evidence from other historical figures in ancient history
While we cannot use evidence from Jesus's resurrection itself to inform its likelihood, we can certainly make use of other notable historical figures or events whose reality are generally agreed on. From a sampling of such instances, we can form an empirical distribution of how much evidence such figures or events can generate. This will then form the basis for the "Christian's distribution".
So, what comparable historical figures from antiquity are there, who might have left evidence of their deeds in some form? Remember, Jesus was not expected to be anyone particularly noteworthy by the standards of his day: he was not a famous politician or a general, nor did he hold any official posts in the religious power structures of the land. He was just an itinerant preacher from nowhere, who started a persecuted movement with some followers.
So, could we compare Jesus with other religious figures of his day? We could. In fact, we've already made this comparison to some degree, in examining the other resurrection stories in non-Christian world history. From there, we saw that Jesus has such an overwhelming amount of evidence for his life and his resurrection that a comparison is almost embarrassing - it's nearly to the point where it would be better for the skeptic to actually argue that Jesus has too much evidence for him.
But let us examine some cases where a resurrection isn't specifically associated with the person in question, and see what we can say about the likely distribution of evidence for Jesus's case.
The Buddha
Gautama Buddha is one such figure, who is sometimes compared to Jesus. But the historical data we have on him is rather scant. The uncertainty around the dates of his birth and death spans nearly a hundred years, and the earliest written account of him only appear one or two centuries after his death. A full biography doesn't appear for a couple hundred years later still. This is inferior in every way compared to Jesus, whose birth and death can each be dated within several years, and written accounts of his life - the New Testament - were written within several decades of his death, within living memory. And yet, since it's generally accepted that the Buddha lived and taught, the amount of evidence for his life and stories must be an acceptable level for such a true historical figure to leave behind. And Jesus beats this by a large margin.
Confucius
Master Kong is more of a philosopher than a religious figure, but there is little controversy about his existence or the basic outline of his achievements. And yet, the amount of evidence for his life and works follows a pattern like the Buddha's: there's the Five Classics, which may have been written or edited by Confucius or his students, but contain little biographical information. The Analects are perhaps the best source of biographical information on Confucius, but they were compiled and edited over a couple hundred years, not taking on their final form until several centuries after Confucius died. Again, given that the basics of Confucius's life and teachings are not in doubt, this must be an acceptable, expected amount of evidence for someone like Confucius to leave behind.
Socrates
Jesus is often compared with Socrates, given that they were both active in the ancient Greco-Roman world. Certainly, many people have made this comparison in many different ways, but of course, we're chiefly concerned about the amount of evidence for their life, and the events surrounding their death.
Here, the record is interesting - Socrates comes to us through a handful of major sources, like Plato and Xenophone. There are also some plays by Aristophanes, but these are works of satire and give us little information on the historical Socrates. There are furthermore other sources which are minor, fragmentary, or late.
This is actually a good amount of evidence. Socrates has excellent, immediate witnesses who wrote about him. Individually, the quality of these witnesses are certainly at least on par with the witnesses of the New Testament: Plato is one of the best possible witnesses, Xenophone is also a well-known historical figure, and there little controversy about their direct connection with Socrates. On the other hand, the New Testament has more numerous witnesses, depending on exactly how you count. There's some modern controversy about their direct connection to Jesus, but the claims in the text itself are clear: they claim to be the work of eyewitnesses, or a consolidation of such eyewitness accounts. Other books in the New Testament are attributed to such eyewitnesses by other ancient sources. Furthermore, the manuscript evidence for the actual text of the accounts is far superior for the New Testament.
In the end, this is one of those issues that Christians and skeptics will go back and forth on, depending on the particulars of how much historical value they put in the New Testament. So perhaps the most that we can say is that Socrates and Jesus are somewhat comparable in the amount of evidence they left in history. Certainly it's not a blowout in one direction or the other: they both come down to a handful of people who claim to have given personal testimonies, and one doesn't have an order of magnitude more in testimonies over the other. This is quite the rabbit hole. So, for the sake of argument, let us be gracious and yield to the skeptic's typical arguments here, and grant Socrates the edge.
What am I doing? At this point, let's remember our goal: it is NOT to make the argument that Jesus had more evidence for his existence than Socrates, or some other historical figure. Others have made that argument, but that's not my purpose here. Rather, my stated goal, from the beginning of this section, is to construct the "Christian's distribution" from empirical, historical data.
The best-case "Christian's distribution" for our Bayesian argument doesn't come from demonstrating that Jesus has more evidence for him than any other attested event in history. Indeed, such a result would actually open up the silly counterclaim that Jesus has too much evidence, that it would be very unlikely for him to have so much. Rather, in order to maximize the likelihood, we need the historical evidence for Jesus and his resurrection to be a TYPICAL amount given the hypothesis, rather than the maximum. Given what we already know about the general shape of the distribution (broad, smooth, no pronounced features, with a slow decay), this maximal likelihood is actually best achieved by having some empirical samples to either side of the amount of evidence for Jesus. Having some samples with less evidence than Jesus, and some with more, makes the amount of evidence for Jesus somewhere in the "middle", meaning it would be a good, typical, and therefore a maximally likely amount.
Tiberius
Keeping this in mind, let's make some more comparisons. How about Tiberius, the Roman emperor at the time of Jesus's ministry? Well, this is clearly an absurd comparison. Jesus was an itinerant preacher, who was executed as a lowly criminal. Tiberius was the absolute ruler of the entire Roman empire, in whose name Jesus was executed. There is no question that there'd be more historical records for Tiberius than for Jesus, nor is this fact particularly helpful in constructing the "Christian's distribution".
But can we somehow modify the comparison to make it useful, by making it more fair? I believe we can. For instance, we can discount the historical records we have for Tiberius which can in no way be expected of Jesus. Here I'm thinking of things like coins minted with Tiberius's name and image, or contemporary inscriptions in public buildings, or formulaic references to the emperor in daily life. Tiberius has these things attesting to him specifically because of his immense political power, because he was the emperor. They can in no way be expected of Jesus.
Excluding such evidence basically leaves us with the literary evidence, of people writing explicitly about Tiberius or Jesus. This gives us something like a measure of the amount of "buzz" that each individual generated, a measure somewhat apart from the amount of institutional power that Tiberius had over Jesus. Of course, such things cannot really ever be completely separated, so this may perhaps only give us a soft upper limit on what we can expect from Jesus.
And what do we find upon making this comparison? That the literary record we have for the two men are surprisingly comparable. We get different results for who comes up on top depending on who's counting what based on what conditions. For instance, Tiberius has a good amount of brief mentions during his own lifetime, which Jesus does not have - but again, this can be mostly chalked up to the enormous political power that Tiberius had as the emperor of Rome. They have about the same number of major ancient biographies about them - four each, again depending on exactly who's counting what. For Tiberius, one of these was written during his lifetime, so again points for that, but this biography is also rather short and full of lavish praise for the then-emperor. Apart from this weak showing, all of Tiberius's other biographies date later than any of the canonical Gospels for Jesus. So Jesus comes out ahead overall on the time gap between the biographies and their actual lifetimes. Of course, as I mentioned before, no ancient text can touch the text of the New Testament in the number of manuscripts we have attesting to their actual text. In total, the number of literary references again vary depending on who's counting what, but whether you believe that the number of literary citations for Jesus vs. Tiberius is 42 to 10 or 37 to 49, or how you choose to value the extent of the writing vs. the date of the composition, all in all this is points at a respectable showing for Jesus.
Again, my goal isn't to show that Jesus had more evidence for his historical existence than Tiberius, nor would that be useful for the Christian case if it were true. The question at hand is how we should construct the "Christian's distribution". And given that the amount of literary sources for Tiberius should serve as a soft upper limit for this distribution, the actual evidence for Jesus is in good agreement with it.
We can make similar arguments with other historical figures. How does the overall historical evidence for Jesus compare with that of Alexander the Great, or Spartacus? How about the accounts of the resurrection event in comparison to, say, Julius Caesar saying "the die is cast" as he crossed the Rubicon, or his assassination in the Roman Senate?
All of these comparisons are hard to make exactly, nor is such a comparison necessary. In each case, after stripping away the kind of evidence which cannot be expected from Jesus, and keeping in mind that financial, military, and political power cannot ever be completely separated from how much people will write about someone, the amount of evidence for Jesus does reasonably well, given his station in life. In all of the above cases, the comparison comes down to some small group of people writing and saying certain things about what happened.
Arguments using the New Testament itself
Lastly, let us consider two additional arguments, which rely on the New Testament itself, and will therefore again be only considered as an extra margin of safety for our overall case for the resurrection.
The first of these starts off from an understanding of the Christ myth theory - the idea that Jesus never existed. This is the flat earth theory of the history of early Christianity. Wikipedia is blunt and brutal in its rejection of the theory, saying that it's a fringe theory that virtually no scholar takes seriously. So, the mainstream historians are well in agreement that a historical Jesus existed, although they differ on what he was like, and the details of his life. So, it must be that the text of the New Testament, as a whole, must provide good evidence for the existence of Jesus. It is neither too much nor too little, given that his existence is not controversial among the scholars. That is to say, if we were to construct a "Christian's distribution" for the existence of Jesus rather than his resurrection, we can be assured that the evidence of the New Testament falls fairly close to the optimum, "typical" value.
And yet, what is the single most important thing that the New Testament teaches about Jesus? That he rose from the dead. The four gospels spend an inordinate amount of their content discussing Jesus's death and resurrection, far more than most other biographies, of anyone. Paul flat-out says that "if Christ has not been raised, our preaching is useless and so is your faith".
Thus, if Jesus actually rose from the dead, the amount of evidence presented in the New Testament must also be fairly close to the optimum, "typical" value for the "Christian's distribution". Since we know that the total evidence for Jesus's existence is not atypical, the same must be true for the total evidence for his resurrection, if it actually occurred. For you cannot expect the total evidence for an event in Jesus's life to exceed the evidence for his overall existence, and yet that is very nearly where we're already at, since so much of the focus of the New Testament is on his resurrection.
The second argument is similar: consider apostle Paul. Now, virtually nobody - not even most of the Christ mythicists mentioned above - doubts Paul's existence. And yet, what is it the most basic, most important thing we know about Paul? That he encountered the risen Christ on the road to Damascus, and thereafter spent his life as Christianity's most effective evangelist. The argument here is analogous to the one above: if the evidence of the New Testament is sufficient to establish Paul's existence, it must also be a reasonable, "typical" value in the "Christian's distribution", as there isn't much more room for Paul to be further dedicated to the idea of Christ's resurrection.
The exact mathematical form of the "Christian's distribution"
So, what can we say from all this?
We know that the "Christian's distribution" must be smooth and broad, with no pronounced peaks or valleys, and with a slow decay. Furthermore, we have the empirical, historical record of other historical figures, which informs us how much evidence we could expect Jesus to leave if he really rose from the dead. Pulling all this together, we can cobble together a satisfactory "Christian's distribution".
First, we note that a number of other religious figures, like the ones whose resurrection we previously considered, left far less evidence for their overall existence than Jesus did. At least some of these were probably at least somewhat historical, and at least some of them should have accomplished some things, even if none of them actually rose from the dead. So, while we cannot use the evidence for their resurrection as a part of the "Christian's distribution", the evidence for their existence does inform us somewhat. And they generally fall far short of the data we have on Jesus.
Recall our x-axis, and that we've set the level of evidence for Jesus's resurrection at x = 6 for now. Then we can say that these religious figures, as a class, argue for having some probability density below x = 1 in our "Christian's distribution". But, of course, we cannot put too much weight on these examples, as many of them probably did not exist at all.
There are other similar figures in history (Honi the circle-drawer, Ichadon, etc.), which we will discuss later. None of them approach anything like the total amount of evidence for Jesus. They all put their weight on having a large amount of probability density at smaller x values.
Among more established historical figures, we have people like the Buddha or Confucius. Their net amount of evidence is below the analogous amount for Jesus, whether you compare them on the totality of historical existence or a specific in their lives. Hence, they also argue for the "Christian's distribution" having some probability density below x = 6, although probably above x = 1.
Once we get to Socrates, we get to a figure who is arguably better attested than Jesus. In fact, just for the sake of this argument, I've already granted that he is. His trial and death were certainly very major events in his life, as Jesus's crucifixion and resurrection was in his. Overall, let's say that this argues for Jesus's resurrection having some probability density at a value somewhat above x = 6.
Next, we get to figures like Emperor Tiberius or Alexander the Great, who cannot be compared directly with Jesus. But after the appropriate treatment, some subset of their evidence can serve as a soft upper limit on what can be expected in the evidence for Jesus's resurrection. While this is quite inexact, such comparisons often result in surprisingly similar results to the actual amount of evidence in Jesus's resurrection, at around x = 6. It's certainly not orders of magnitude above that.
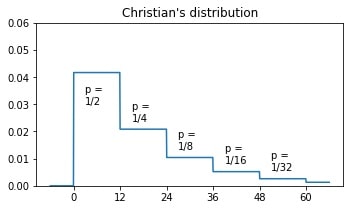
Pulling all this together, I propose the following for the "Christian's distribution".
Half of the probability will be uniformly assigned between in a block from x = 0 to 12. Thereafter, for each block of 12 units in x, half again as much as the previous block will be uniformly assigned to those x values. The distribution will thus decay in a geometric fashion, out to infinity.
Now, let us see how this distribution fares in the face of possible objections to it.
The robustness of the Christian's distribution
First, let's see how our distribution corresponds to the historical data. By comparing Jesus with similar historical figures (the Buddha, Confucius, Socrates, Apollonius et al., etc.), we saw that the "Christian's distribution" should largely have its probability density below x = 6, although some significant chunk of it should be above that. But our distribution actually does more in favoring the skeptic: it's median value is at x =12. Only half of the probability density is below that, and the other half above it. Its mean value is even greater, out at x =18.
In comparison to figures like Tiberius, we saw that the Christian's distribution should have its a soft upper limit at an x value in the ballpark of x = 6. But again, this distribution does better: it assigns an appreciable amount of probability to an x value a full order of magnitude above that, at x = 60, while extending out to infinity. Our distribution gives about a 3 percent chance (1/32) for Jesus's resurrection to give ten times more evidence than what we've been considering. Small, to be sure, but certainly not impossible or unrealistic.
So, if a skeptic were to demand that Jesus's resurrection ought to have resulted in ten times more evidence, which is completely out of scope with any comparable figure in history, we could simply look at our distribution and say, "yup, that might have been unlikely, but it was certainly possible". We need not adjust anything of our calculation or conclusion in the face of such assertions. In fact, even if this case was made with the solid historical backing of someone comparable with Jesus actually yielding that level of documented evidence, as long as it was just a few isolated incidents we need not change anything. Our distribution is already generous enough to the skeptic's cause to account for it effortlessly.
Let us take a moment and enumerate what "ten times more evidence" is. That would mean ten different crowds of 500 people each who are said to have witnessed the risen Christ. It would mean ten different figures like the Apostle Paul, each of whom were initially skeptical of the resurrection to the point of actively persecuting Christians, who then had a miraculous encounter with Jesus and became an ardent evangelist for Christianity. Ten different sets of the Twelve disciples, including preeminent figures like Peter and John, giving their testimony, laid out in a set of forty different Gospels, each at least somewhat different from the other. There is nobody in the ancient world, with a background comparable to Jesus (an itinerant preacher with no official, institutional power who lived in a backwater regions of a major empire), who approach anywhere near this level of evidence for any event in their lives. And yet, our distribution is so generous to the skeptic's case that it even allows for, and seamlessly incorporates, the ridiculous demand for there to be this much evidence for Jesus's resurrection.
But what if a skeptic were to become completely unhinged from any concern for historical data, and started making insane demands? Say that someone demands that the distribution be completely flat over the range of x = 0 to 60. We will simply ignore the fact that all historical precedents say that the Christian's distribution should be concentrated at the smaller x values, and that a value of x = 60 is ridiculous. Even so, this will not materially change our final conclusion.
Recall that the whole reason for constructing the "Christian's distribution" is to combine it with the "skeptic's distribution", to get an order-of-magnitude estimate of the Bayes factor. That "order-of-magnitude" nature of our calculation is important. With our current distribution, at x = 6, the value of the probability density is 0.5/12 ≈ 0.0417. But if we were to flatten the whole distribution to be uniform across 0 to 60, the probability density would then be 1/60 ≈ 0.0167. So, the result of acquiescing to even this ridiculous demand results in a change by less than a factor of 3 - which is less than half an order of magnitude, which is literally a rounding error in an order-of-magnitude calculation.
Indeed, this gives us a way to calculate the following: what would it take to meaningfully change the final results, by challenging our "Christian's distribution"? Well, that would mean changing the result by more than a single order of magnitude. Which means that at values around x = 6, we need the "Christian's distribution" to be more than ten times smaller than our currently proposed distribution. Since the overall properties of the distribution must be preserved - broad, smooth, no pronounced features, slowly decaying - the only way to achieve this is to stretch out the distribution along the x axis by a factor of 10.
Recall that our current distribution was able to effortlessly incorporate a demand for 10 times more evidence, at x = 60. Stretching it out by a factor of 10 would allow it to have appreciable probability out at x = 600. In other words, this is equivalent to accommodating the absolutely ludicrous demand that Jesus's resurrection should have resulted in a hundred times more evidence than what we're currently discussing.
But you know what? If the skeptic can provide the historical evidence for this demand, then he will have made his case. He will need to provide historical examples of individuals comparable to Jesus, who had a hundred times more evidence for an event in their lives than Jesus has for his Resurrection. Note that a few isolated examples will not do: a stretch by a factor of 10 can incorporate such data effortlessly. No, in order to force the results to change by more than an order of magnitude, the skeptic must not only show that such individuals existed, but that such level of evidence were the norm for these individuals.
Again, let's take a moment to appreciate what a value of x = 600 actually means. That's a hundred times more evidence than what we have for Jesus's resurrection. If it's applied directly to Jesus, it would correspond to him effectively sticking around on Earth for the last 2000 years, and publicly showing himself every two decades to demonstrate that he's still alive, generating a new crop of New Testament level primary-source witnesses each time. It's having 400 separate biographies on par with the Gospels, all written within a human lifetime of the person in question. It's a hundred people like Apostle Paul, each with a firsthand, miraculous witness testimony about the events in question, each of which cause a fundamental, lifelong change in the witness. It's an absolutely absurd amount of evidence.
If anyone can demonstrate that ancient historical figures comparable to Jesus (persecuted itinerant preacher, no institutional power, in backwater regions) regularly generated this level of evidence as the norm, then I will reconsider my "Christian's distribution". Such data would change the final results by more than an order of magnitude, and at that time I will incorporate that data and adjust my "Christian's distribution" accordingly.
Failing that, we have our "Christian's distribution", which will use in our proceeding calculations.
The calculation plan
Let us bring together everything we've said thus far about the "skeptic's distribution" and the "Christian's distribution", and lay out how we'll approach this calculation.
We assume that the "skeptic's distribution" will take the form of a linear combination of generalized Pareto distributions, distributed over different possible shape parameters. This distribution over the shape parameters will be determined in turn by the number of "outliers" in history.
A resurrection report is considered an "outlier" if it has at least 50% of the evidence compared to the maximum evidence among the non-Christian resurrection reports. All the "some people say..." type of resurrection stories, like the ones we mentioned earlier, belong to this "outlier" class. The number of such "outliers" in history determines the distribution of shape parameters, which in turn determines the "skeptic's distribution"
As for the "Christian's distribution", we already have a specific function, which we know to be incredibly robust. We will simply use that function.
Once we have these two distributions, we simply need to compare them: the ratio of the distributions at the x value corresponding to the actual amount of evidence for Jesus's resurrection (say, at x = 6) will determine the Bayes factor.
We will write a computer simulation to do all this. Here are the specs for the program.
For the "skeptic's distribution", we will consider shape parameters at regularly increasing intervals from 0.01 to 2.0. Our region of interest will lie in this range.
We will create a generalized Pareto distribution with that shape parameter, then simulate drawing the maximum value of 1e9 samples from that distribution. We will re-scale the distribution to set that maximum at x = 1, then get the probability density at x = 6 and the number of outliers.
We will do this many times for each value of the shape parameter. This gives us a table with a great number of rows, with each row containing the shape parameter, the number of outliers, and the probability of generating a Jesus-level of amount of evidence.
If we assume equal prior weights for each of the shape parameters, we can consider the final, posterior distribution of the shape parameters to be just its distribution from the subset of the table where the number of outliers is equal to the actual, historical value. That is to say, we just have to look at where the theory fits the data, and consider only those theories. This satisfies Bayes' theorem, as we're effectively just using a hierarchical Bayes model.
Our "skeptic's distribution" is then just the average of these distributions over that subset. Once we have this distribution, getting the final Bayes factor just requires taking the ratio between it and the "Christian's distribution", as mentioned earlier. The final output of the program will be the Bayes factor, given the number of historical "outliers" as an input.
All of the assumptions and choices made above favors the skeptic's case. Therefore, the Bayes factor obtained at the end will be a minimum value.
Simulation and code: The number of "outliers" decides the case.
This is a jupyter notebook. It contains the python code which generates the relationship between the number of "outliers", and the Bayes factor of the evidence for Jesus's resurrection.
%matplotlib inline import numpy as np import pandas as pd from scipy.stats import genpareto, binom
def max_out_of_n_from_dist(dist, out_of_n=1e9):
manageable_n = 100000
if out_of_n <= manageable_n:
return dist.rvs(out_of_n).max()
else:
top_percentiles =
np.random.rand(manageable_n) * manageable_n / out_of_n
return min(
dist.isf(top_percentiles.min()),
np.finfo(float).max / 100) # prevent inf
We then simulate getting the maximum value out of 1e9 samples drawn from these distributions, and rescale the distribution so that this maximum value is at x = 1. Then we calculate the probability density at x = 6. This is the likelihood of drawing a sample at 6 times the maximum value - that is to say, the likelihood of "naturally" generating a Jesus-level resurrection report from this distribution. Lastly, we next calculate how many "outliers" would exist in this distribution.
We repeat this 10000 times for each of the 200 shape parameters between 0.01 and 2.0, and put it all in a table. The result is a table with 2 000 000 rows, whose columns are the shape parameter, the likelihood of drawing a sample 6 times greater than the maximum, and the number of "outliers".
The following code gives us this results table.
sample_size = int(1e9)
genpareto_shapes = np.linspace(0.01, 2.0, 200)
shape_params = []
pdf_6x_max = []
n_outliers = []
for shape_param in genpareto_shapes:
dist = genpareto(shape_param, scale=1, loc=0)
for i in range(10000):
shape_params.append(shape_param)
max_val = max_out_of_n_from_dist(dist, sample_size)
scaled_dist = genpareto(
shape_param, scale=1 / max_val, loc=0)
pdf_6x_max.append(scaled_dist.pdf(6))
# use binom instead of actually drawing for outliers
p_outlier = (
scaled_dist.sf(0.5) - scaled_dist.sf(1)
) / scaled_dist.cdf(1)
n_outlier =
binom(sample_size - 1, p_outlier).rvs(1)[0] + 1
n_outliers.append(n_outlier)
genpareto_results_df = pd.DataFrame({
"shape_params":shape_params,
"pdf_6x_max":pdf_6x_max,
"n_outliers":n_outliers,
})
#save to .csv, as generating this takes a while
genpareto_results_df.to_csv(
"genpareto_results_df.csv", encoding="utf-8")
genpareto_results_df = pd.read_csv(
"genpareto_results_df.csv", encoding="utf-8"
).drop("Unnamed: 0", 1)
print(genpareto_results_df.shape) genpareto_results_df.head()
(2000000, 3)
| shape_params | pdf_6x_max | n_outliers | |
|---|---|---|---|
| 0 | 0.01 | 1.400046e-36 | 26287 |
| 1 | 0.01 | 1.650500e-38 | 11942 |
| 2 | 0.01 | 4.315781e-36 | 31962 |
| 3 | 0.01 | 2.588130e-37 | 19289 |
| 4 | 0.01 | 3.339785e-39 | 8680 |
How could we get this posterior distribution of the shape parameters? All we need to do is to take the subset of the results table where the number of outliers is exactly 15, and look at the shape parameters. This satisfies Bayes' theorem, and the distribution of shape parameters in that subset IS the posterior distribution for the shape parameter.
Let's write a function to do this and see what it looks like:
def shape_hist(df, n_outliers):
srs = df[df["n_outliers"] == n_outliers]["shape_params"]
n_bins = (srs.max() - srs.min()) / 0.01 + 1
srs.hist(bins=int(n_bins)).set_xlabel("shape parameters")
shape_hist(genpareto_results_df, 15)
Continuing on with the same reasoning, the "skeptic's likelihood" of generating a Jesus-level resurrection report would simply be the density of that distribution at x = 6. Since we tracked this value in the above table, again all we have to do is take the subset of the table where the number of outliers is exactly 15, and average over this likelihood value.
Furthermore, the Bayes factor is simply the ratio of this value to the the likelihood from the "Christian's Distribution", which is just 0.5/12 for values up to x = 12.
As before, let's write a function to calculate these values, to see what they are with 15 outliers:
def likelihood_and_bf(df, n_outliers):
skeptical_likelihood = df[
df["n_outliers"] == n_outliers]["pdf_6x_max"].mean()
christian_likelihood = (0.5 / 12)
bf = christian_likelihood / skeptical_likelihood
print("skeptic's likelihood: {:.2e}"
.format(skeptical_likelihood))
print("Bayes factor: {:.2e}".format(bf))
likelihood_and_bf(genpareto_results_df, 15)
skeptic's likelihood: 8.51e-12 Bayes factor: 4.90e+09
Of course, there's almost certainly more than 15 outliers in world history. This further forces the shape parameters to smaller values. In addition, this distribution over shape parameters turns out to decay quite rapidly as it goes off to the right (demonstrating this is left as an exercise to for the reader). All this combines to show that the upper limit of 2.0 will have no bearing on our conclusions.
shape_hist(genpareto_results_df, 60)
likelihood_and_bf(genpareto_results_df, 60)
skeptic's likelihood: 3.86e-13 Bayes factor: 1.08e+11
shape_hist(genpareto_results_df, 250)
likelihood_and_bf(genpareto_results_df, 250)
skeptic's likelihood: 1.44e-14 Bayes factor: 2.90e+12
outliers_pdf_6x = genpareto_results_df[
genpareto_results_df["n_outliers"] < 100
].groupby("n_outliers")["pdf_6x_max"].mean()
outliers_pdf_6x.name = "pdf_6x_max"
outliers_pdf_6x.reset_index().plot(
kind="scatter", x="n_outliers", y="pdf_6x_max",
xlim=(0,100), ylim=(0, 6e-11),
title="skeptic's likelihood vs outliers"
)
outliers_log10_bf = np.log10((0.5 / 12) / outliers_pdf_6x)
outliers_log10_bf.name = "log10_bf"
outliers_log10_bf.reset_index().plot(
kind="scatter", x="n_outliers", y="log10_bf",
xlim=(0,100), ylim=(8, 14),
title="Bayes factors vs outliers"
)
Otherwise, looking at the graphs above, we see that the skeptic's likelihood of generating a Jesus-level resurrection report drops as the number of "outliers" increases, thereby increasing the Bayes factor. Having MORE non-Christian resurrection reports (that is, having more "outliers") makes the skeptic LESS able to explain Jesus's resurrection, and therefore makes it MORE likely - exactly as we said before.
So, the question now just comes down to this: how many "outliers" can we find in world history? Recall that anyone with a "some people say..." level of evidence for their resurrection counts as an outlier. The more such people we find, the more firmly Christ's resurrection is established. Can we find enough such people to overcome the low prior probability against a resurrection?
Putting Jesus's resurrection over the top: the list of outliers
Here is a partial list of "outliers", including the ones we have already covered:
Aristeas (ancient Greek Poet)
Apollonius of Tyana (ancient Greek philosopher)
Krishna (Hindu god)
Zalmoxis (ancient Getae god)
Osiris (ancient Egyptian god)
Dionysus (ancient Greek god)
Bodhidharma (Buddhist monk)
Puhua (Buddhist monk)
Horus (ancient Egyptian god)
Ba'al (Canaanite god)
Melqart (Phoenician god)
Adonis (ancient Greek god)
Eshmun (Phoenician god)
Tammuz (Sumerian god)
Ishtar (Sumerian goddess)
Attis (Phrygian god)
Quetzalcoatl (Aztec god)
Parashurama's mother (character in Hinduism)
Sisyphus (character in Greek mythology)
Pelops (character in Greek mythology)
Persephone (ancient Greek goddess)
Asclepius (ancient Greek god/healer)
Hippolytus, son of Theseus (character in Greek mythology)
Achilles (ancient Greek hero)
Memnon (ancient Greek hero)
Castor (character in Roman mythology)
Alcmene (character in Greek mythology)
Heracles (ancient Greek hero)
Melicertes (character in Greek mythology)
Romulus (mythic founder of Rome)
Cleitus (character in Greek mythology)
Cycnus, king of Kolonai (character in Greek mythology)
Cycnus, friend of Phaethon (character in Greek mythology)
Odin (Norse god)
Augustus (Roman emperor)
Peregrinus Proteus (ancient Greek philosopher)
Rabbit Boy (character in native American mythology)
Arrow Boy (character in native American mythology)
Man-eagle (character in native American mythology)
Judah the Prince (Jewish rabbi)
Sabbatai Zevi (Jewish rabbi, messiah claimant)
Kabir (Indian mystic poet)
Calybrid and Calyphony (characters in Celtic myth)
Muisa (character in a Nyanga epic)
People of Tubondo (characters in a Nyanga epic)
Hebo (Chinese god)
Li Tieguai (Chinese immortal)
Zhang Guolao (Chinese immortal)
People resurrected by Zhongli Quan (associates of a Chinese immortal)
Ye Fashan (Chinese immortal)
Zhong Kui (Chinese demon hunter)
Miaoshan (incarnation of Buddhist bodhisattva Guanyin)
Ganesha (Hindu god)
Daksha (Hindu god)
Brahma (Hindu god)
Kacha (Hindu sage)
Shukra (Hindu sage)
Jvarasura (Hindu god)
Capaneus (character in Greek mythology)
Tyndareus (character in Greek mythology)
I'm going to stop here - not because I've come anywhere near to exhausting such "outliers", but because this is quite enough. The above list contains 60 people (or groups of people) who are claimed to have been "resurrected" in some form, with about a "some people say..." level of evidence behind them. And as we saw previously in the jupyter notebook, 60 outliers is enough to raise the Bayes factor for Jesus's resurrection above 1e11.
Combining that with the prior of 1e-11 against the resurrection gives a number bigger than 1e0. That is, Jesus's resurrection has better than even odds of having occurred.
Notice that the procedure up to this point outlines the worst case scenario for the resurrection. For example, I stopped the above list of "outliers" at 60 only because it was getting tedious to write more. Each member of the above list was obtained with just a little bit of research, mostly from stories that are readily available online, accessible to a culturally western, English-speaking audience. If you enjoy studying mythologies, you'll often just run into such stories without even trying. How many such "outliers" are there in total, throughout all of world history? How many stories where "some people say..." that someone rose from the dead? I would imagine it to be easily in the hundreds, if not thousands.
So, "better than even odds" is the absolute minimum that can be said for Christ's resurrection. We will next see how much more can be said about it.
We were far too generous for the "skeptic's distribution"
We have established that the resurrection has, at a minimum, even odds of having taken place. Now, let us retrace our steps, go back over the procedure that got us to this point, and demonstrate that the worst case scenario for the resurrection had in fact been assumed at every point.
The power law distribution
Looking back, we see that our first decision was to choose a power law as the form of the "skeptic's distribution". As I mentioned when we made the choice, this is the most pro-skeptical choice we can make which still fits the facts. Power law distributions have one of the longest possible tails, which can decay very slowly. They're fully capable of a "black swan" event. Furthermore, they're ubiquitous in human behavior, in that they're naturally generated when an increase in a value depends on the value itself. For this reason, the distributions of personal wealth, city sizes, and website popularity all follow a power law distribution. It's therefore appropriate to use it to model the buildup of evidence through possibilities like conspiracy theories or religious mass delusions.
However, there are excellent reasons to believe that the true "skeptic's distribution" will die off more quickly than a power law distribution, especially when we extrapolate it to 6 times the maximum observed value. You see, few real-life power law distributions can actually extend off to infinity. Some external factor will intervene to cut off the distribution at very large values.
Consider the example of city sizes. The population of cities follows a power law, and this holds up pretty well as long as we consider populations up to tens of millions of people. However, if we try to extend this out to infinity, the distribution no longer holds. We run into external factors which limit city sizes, such as the total population of the country or the logistics of city growth in a given geography. For example, the largest city in South Korea is Seoul, with about 10 million people. A city 6 times larger than that would have over 60 million people - larger than the total population of South Korea, which is only 50 million. Such a South Korean city cannot exist - not because its probability would be too small according to the power law distribution, but because it runs into external factors, like the fact that a city cannot be larger than the country to which it belongs. That is to say, the power law distribution for city sizes is limited, or cut off, at the long tail.
You can imagine similar arguments for personal wealth and website popularity. An individual cannot actually have "all the money in the world", and a website cannot be linked from more websites than the number that actually exist. And even far before such limits, sociological effects will likely truncate the distribution's long tail. Likewise, naturalistically generated evidence for resurrection stories cannot follow a power law distribution out to infinity. Other, external factors will cut off or strongly attenuate the probability as such resurrection stories gains more momentum.
For this reason, the true "skeptic's distribution" is almost certainly something that looks like a power law over the actually existing samples, but decays more quickly thereafter. A number of distributions - like a log-normal distribution or a power law with an exponential cutoff - follow this behavior, and are also very common in human behavior. In each case, these other distributions with their "shorter" tails would help the case for Christ's resurrection. So adopting a generalized Pareto distribution, which is a genuine power law all the way out to infinity, was the most pro-skeptical choice we could have made.
The uniform distribution over shape parameters
Next, we used evenly-spaced shape parameters for our distribution. That is to say, we chose a uniform distribution over the shape parameter as our prior. Again, this almost certainly unduly favors skepticism. Consider what such a prior distribution means: the true shape parameter would be 1000 times more likely to be between 1000 and 2000 than between 0 and 1. It would be infinitely more likely to be greater than 1 than to be less than 1. Remember that a larger shape parameter favors the skeptic's case, and we have chosen a prior that favors these larger values. It is only through the weight of the evidence that this prior distribution gets reigned in, but choosing such a prior in the first place still biased the end results.
A more common choice of prior in such circumstances is to consider shape parameters which increase linearly in their logarithms. For example, we may consider shape parameters like 0.01, 0.1, 1, 10, 100, and so on. The idea is that we don't know what the order of magnitude of the shape parameter would be, and therefore consider each order of magnitude equally. Of course, such a prior favors the smaller shape parameters compared to the uniform distribution that we actually used, meaning that it helps the case for the resurrection. So once again, our choice of evenly-spaced shape parameters was the most pro-skeptical choice we could have made.
The sample size, in the number of reportable deaths
Next, we considered the maximum value of 1e9 samples drawn from our "skeptic's distribution". That value of 1e9 was chosen as the number of "reportable deaths" in world history. That is, this is the number of deaths that had a chance to be witnessed, documented, or told about in a story. It excludes those deaths where nobody could have made a statement about that death, even if a genuine resurrection took place.
But a moment's reflection shows that this number is too small. Only 1e9 - one billion - "reportable deaths" in world history? More people than that have died just in the last century, and virtually all of these deaths have been "reportable" according to the definition above. Surely a more realistic figure would easily be above 1e10.
This is important, because this value effectively sets an upper bound on the probability of generating a Jesus-level resurrection report. A report with the most evidence out of 1e9 samples has a probability of about 1e-9 of being generated. The most evidence out of 1e10 samples would correspondingly have a probability around 1e-10. We are then calculating the chances of generating a report with 6 times more evidence.
It's clear that the larger the number of samples, the smaller the probability of generating a report with a level of evidence comparable to the maximal sample. The probability of beating that by a factor of 6 is smaller still. So, the more samples we use, the smaller the probability for the "skeptic's distribution" generating a Jesus-level resurrection report. In other words, using 1e9 as the number of "reportable deaths" was a pro-skeptical choice. The true value is definitely much larger - probably above 1e10. And using this true value would only strengthen the case for the resurrection.
The boundaries of outliers
We've defined "outliers" as any resurrection report falling in the range of 0.5 to 1.0. This is well and good, but all the actual outliers may in fact be clustered in a narrower range. In particular, the x = 1 point was defined as "the amount of evidence associated with the single most convincing non-Christian resurrection report in world history". But after surveying the historical record, it's clear that we have no such thing. We have a number of contenders, but no clear, singular front-runner.
This indicates that even the best non-Christian resurrection report falls distinctly short of the x = 1 point. This narrows the range over which our outliers actually exist, and thereby pushes up more on the x < 1 left side of the "skeptic's distribution". The end result is that the "more outliers makes Jesus's resurrection more likely" argument is further strengthened.
The number of outliers
Of course, the number of outliers was a lower bound as well. I've already touched on this - we used 60 as the number of resurrection reports with a "some people say..." level of evidence, because we cited 60 specific examples. But this is bound to be a vast underestimate. It comes from a very limited subsample of all the stories in world, mostly reachable by just a few minutes of online research in English. The true number of such outliers may easily be in the hundreds or thousands. So this, too, was chosen to favor the skeptical case.
The factor by which we exceeded the fixed point
Next, consider the factor of 6 that we used, as the ratio between the level of evidence in Jesus's resurrection, and our fixed point of "once in non-Christian world history". This, too, was a very conservative estimate, which favors the skeptic's case.
This is laid out in the initial graph of the partial histogram. The factor of 6 came from the fact that there were 6 separate components to the summary of evidence in 1 Corinthians 15, and that non-Christian world history has failed to even come close to matching any one of these components. But we don't know exactly how far they fall short by, except to say that it's by a lot.
Taken step by step, it goes like this: we start at our fixed point of 'once in non-Christian world history', at x = 1. Far greater than this level of evidence is the weakest of the 6 components - the testimony of 500 witnesses. We know this because this is the component that the record of non-Christian world history comes closest to matching, yet it falls far short of it. So, the non-Christian world history fails to even come close to this weakest of the 6 components, which in turn is quite far below the average value of all the components in 1 Corinthians 15. And the total evidence in 1 Corinthians 15 is 6 times this average value. Altogether, this shows that the level of evidence between "once in non-Christian world history" and Jesus's resurrection is significantly greater than 6. Using 6 as the factor is a very conservative, pro-skeptical choice.
A better estimate of the probability
So we see that "even odds" for Jesus's resurrection is not really even the minimum - it's essentially an impossibility. It's a value derived by severely discounting and ignoring huge realms of evidence for the resurrection, while granting the skeptic's case all reasonable (and some unreasonable) allowances. The actual odds would be far more favorable towards Christianity.
Let us run some the calculations to get an estimate of these "actual odds".
The simulation and code, revisited with more likely values
This is another Jupyter notebook. It contains python code that calculates the Bayes factor for the evidence of Jesus's resurrection.
import numpy as np import pandas as pd from scipy.stats import lognorm, genpareto, norm
def max_out_of_n_from_dist(dist, out_of_n=1e9):
manageable_n = 100000
if out_of_n <= manageable_n:
return dist.rvs(out_of_n).max()
else:
top_percentiles =
np.random.rand(manageable_n) * manageable_n / out_of_n
return min(
dist.isf(top_percentiles.min()),
np.finfo(float).max / 100) # prevent inf
def norm_redraw(mu, sigma):
draw = int(round(norm(mu, scale=sigma).rvs(1)[0]))
if draw <= -1:
return norm_redraw(mu, sigma)
else:
return draw
def calculate_bf(
dist_type, #genpareto or lognorm
shape_params_dist, #np.geomspace or np.linspace
sample_size, #1e9 to 1e10+
greater_by, #6 to 10+
outlier_interval, # (0.5, 1) to (0.5, 0.9)
n_historical_outliers, #60 to 300+
n_max_draws=10000,
):
if dist_type == genpareto:
shape_limits = [0.01, 2.0]
elif dist_type == lognorm:
shape_limits = [0.1, 10.0]
shape_params_list = shape_params_dist(
shape_limits[0], shape_limits[1], 200)
shape_params = []
pdf_greater_by = []
n_outliers = []
for shape_param in shape_params_list:
dist = dist_type(shape_param, scale=1, loc=0)
for i in range(n_max_draws):
max_val = max_out_of_n_from_dist(dist, sample_size)
scaled_dist = dist_type(
shape_param, scale=1 / max_val, loc=0)
# approximate binom with norm
p_outlier = (
scaled_dist.sf(outlier_interval[0])
- scaled_dist.sf(outlier_interval[1])
) / scaled_dist.cdf(1)
mu = (sample_size - 1) * p_outlier
sigma = (
(sample_size - 1)
* p_outlier * (1 - p_outlier)) ** 0.5
n_outlier = norm_redraw(mu, sigma) + 1
if n_outlier == n_historical_outliers:
n_outliers.append(n_outlier)
shape_params.append(shape_param)
pdf_greater_by.append(scaled_dist.pdf(greater_by))
result_df = pd.DataFrame({
"shape_params":shape_params,
"pdf_greater_by":pdf_greater_by,
"n_outliers":n_outliers,
})
if result_df.shape[0] < 50:
print("warning: result_df.shape = ", result_df.shape)
if result_df["shape_params"].max() == shape_params_list.max():
print("warning: maxed out shape_param")
bf = (0.5 / 12) / result_df["pdf_greater_by"].mean()
print("Bayes factor: {:.2e}".format(bf))
calculate_bf(
dist_type=genpareto,
shape_params_dist=np.linspace,
sample_size=int(1e9),
greater_by=6,
outlier_interval=(0.5, 1),
n_historical_outliers=60,
)
Bayes factor: 1.06e+11
The sample size (that is, the number of reportable deaths in world history): from 1e9 to 1e10.
The multiplicative factor between the level of evidence in 1 Corinthians 15 and the "once in non-Christian world history" level: from 6 to 7
The number of "n_historical_outliers" (That is, the number of reports of a "resurrection", with at least a "some people say..." level of evidence): from 60 to 200.
All of these changes are almostly certainly true to at least that extent. The actual truth may be even more extreme - for example, the number of outliers may actually be in the thousands.
This gives a very conservative answer for the Bayes factor.
calculate_bf(
dist_type=genpareto,
shape_params_dist=np.linspace,
sample_size=1e10,
greater_by=7,
outlier_interval=(0.5, 1),
n_historical_outliers=200,
)
Bayes factor: 1.12e+14
calculate_bf(
dist_type=lognorm,
shape_params_dist=np.geomspace,
sample_size=int(1e10),
greater_by=8,
outlier_interval=(0.5, 1),
n_historical_outliers=300,
)
Bayes factor: 8.41e+15
calculate_bf(
dist_type=lognorm,
shape_params_dist=np.linspace,
sample_size=int(1e10),
greater_by=8,
outlier_interval=(0.5, 0.9),
n_historical_outliers=200,
)
Bayes factor: 3.80e+14
calculate_bf(
dist_type=genpareto,
shape_params_dist=np.linspace,
sample_size=int(2e10),
greater_by=10,
outlier_interval=(0.5, 0.95),
n_historical_outliers=250,
)
Bayes factor: 6.12e+15
calculate_bf(
dist_type=lognorm,
shape_params_dist=np.geomspace,
sample_size=int(2e10),
greater_by=10,
outlier_interval=(0.5, 1),
n_historical_outliers=200,
)
Bayes factor: 1.14e+16
So, those are some of the possible values for the "skeptic's probability". We see that the Bayes factor of 1e11 was an impossible best-case scenario for skepticism. A very conservative - but not fantastical - value would be more like 1e14, and a somewhat conservative scenario gives values beyond 1e16. Against a prior of 1e-11, this results in a posterior probability of 99.9% (very conservative) to 99.999% (somewhat conservative) for the resurrection. Is that our final value?
Not yet. Notice that throughout this whole "skeptic's distribution" argument, I've never brought up Paul's independence from the rest of the disciples? This is a huge point in favor of the resurrection which has been simply ignored. Let us next address this point, and others like it.
The pro-resurrection arguments we have yet to consider
On top of that, our entire argument about the "skeptic's distribution" only takes the AMOUNT of evidence into account. It argues that no possible effect - not even the ones with a near-total dependence in the evidence (e.g. conspiracy theories) - could falsely generate the amount of evidence for Jesus's resurrection.
Recall that nearly all of the remaining possibility for the skeptic was in crackpot theories like conspiracies. Without such theories, their probability values drop to ridiculous numbers like 1e-43. So these specifically anti-crackpot properties in the resurrection testimonies are a direct body blow against the skeptic's remaining case. They apply nearly their entire weight against the remaining probability for the skeptic.
So we expect these anti-crackpot properties to significantly shift the final odds. Let us examine them one by one.
Defenses against crackpot theories built in to Christianity
Could the resurrection testimonies really have a near-total dependency among them? Could they have been generated by a conspiracy of some sort? There are a multitude of reasons to think they were not.
Apostle Paul
First, there is the story of apostle Paul, whose independent nature we've already discussed up in "the basic argument" section. He's one of the named witnesses in 1 Corinthians 15, and someone who first started out as a zealous persecutor of Christianity. He is then supernaturally converted by literally seeing the light on the road to Damascus, and becomes Christianity's most effective evangelist. How many conspiracies have something like that in their narrative?
Now, the conspiracy theorist can still say "that was obviously a part of the plan! You've been taken in by their trap!" After all, that's precisely what a conspiracy theory is designed to do. But as I said before, while this allows them to "explain" apostle Paul by keeping the Bayes factor for his testimony to around 1, it is still a significant blow against a conspiracy theory. For a conspiracy that has planned for such a conversion is a priori far less likely than one that has not. In postulating a deeper, vaster, and more comprehensive conspiracy, the theorist has postulated a less likely one.
In fact, Paul's conversion is so unlikely that it's probably enough by itself to debunk the most common types of crackpot theories. Ascribing Paul's actions to a conspiracy is like planning to punch a stranger in the streets in hopes of making money from the ensuing lawsuit, or asking a politician to concede an already won election to their bitter rival solely out of respect and goodwill. The odds of success for such schemes are long indeed. Humans just don't work that way.
Apostle James
But we're just getting started. Let's look at James - the biological brother of Jesus, and another of the named witnesses in 1 Corinthians 15. Consider his relationship with the rest of the early Christian movement. Earlier on in Christ's ministry, there is good reason to think that there were some strained relationships between his family and his disciples. And yet, after the resurrection James is considered one of the chief disciples, and is named as a witness to Christ's resurrection. Could this have been the result of a conspiracy?
Unlikely. Family members and professional associates often form disparate circles, and it would be an additional obstacle for a conspiracy to grow to encompass that divide, especially if it involves an estranged family member. Of course, you can postulate that James was in on the plan from the beginning - but you're again just postulating a bigger, and therefore a less likely, conspiracy.
So there is already a great deal of independence for Paul and James from the rest of Jesus's disciples, which include Peter. So our three named witnesses in 1 Corinthians 15 are quite unlikely to be dependent, and therefore their testimonies are unlikely to be the product of a conspiracy.
The diversity among the 12 disciples
But the independence of the witnesses don't stop here. The twelve disciples may be thought of as a fairly interdependent group - after all, they were twelve Jewish males who all followed one leader. But looking into their background reveals a good amount of diversity. Some of them were fishermen - but their number also included, at a minimum, a tax collector (working for Rome) and a zealot (revolutionaries working against Rome). It's not easy to come up with three groups that would have gotten along less with each other than a tax collector, a zealot, and a regular Jewish worker, like a fisherman. Could a conspiracy rise from such a group? Again, it's not impossible, but it's also not likely.
The diversity among the earliest converts
The diversity is further magnified in the earliest converts to Christianity, at the Pentecost. According to Acts 2, these people were from all over the known world. Many of them did not even consider Hebrew, Aramaic, or Greek to be their native tongue. Again, could a conspiracy spread out so quickly to such a diverse group, as the very first people to be taken in? It must have been a very flexible and compelling conspiracy indeed - and therefore a very unlikely one.
The inclusion of women
Lastly on the point of diversity, there are of course the women. They go unmentioned in the public declarations of 1 Corinthians 15, because women were not considered reliable witnesses in the 1st century Jewish society. Yet they are featured prominently in the actual narrative in all of the Gospels - as the group that did not abandon Jesus at the cross, and the first witnesses to the risen Christ. What kind of conspiracy does this? Why have the first witnesses to the resurrection be a class of people the society considers unreliable? Why include them in the story at all, if you're not going to publicly mention them among the chief witnesses?
If it's all true, then this all makes sense. But as a conspiracy theory, each one is a mystery. One can construct a conspiracy theory that fits all this, but such a conspiracy would be a rare one indeed, and highly unlikely a priori.
The divisions in early Christianity
So the diversity of the individuals involved in Christ's resurrection testimonies already make a high degree of interdependence unlikely. One could hardly find a less likely group of people to enter into a world-spanning conspiracy. You would expect disparate parts of such a group to be constantly at odds with each other, destroying the conspiracy almost immediately.
In fact, that's pretty much what happened: the disparate parts of the group were constantly at odds with each other - and yet, the "conspiracy" was preserved.
There were hints of confusion and division even before Jesus's crucifixion, in things like the disciples arguing about who will be the greatest, or who will be sitting by Jesus's side when he establishes his kingdom. Peter even berated Jesus for announcing his upcoming death, and there seems to have been a general confusion about the nature of the movement - are they going to lead an uprising against Rome? Do they need to be armed?
After Christ's ascension, very early in the book of Acts, there was a conflict between the Greek-speaking members and the other Jewish members of the Church, concerning the equitable distribution of food to their widows. This was a big enough deal that the Church instituted a whole new tier of leadership - the first deacons - to address the issue. And yet, the central tenant of the "conspiracy" - the resurrection - was unchanged.
Persecution and further division
Soon thereafter, an intense persecution befell the church. Several key members were killed, and the church was scattered across the known world. Gentiles were first evangelized around this time as well (Cornelius, Ethiopian eunuch) - which in itself caused no small amount of controversy. All of this further fragmented an already very diverse church. The problem was so bad that various evangelists regularly encountered people with very incomplete knowledge about Jesus. There was a group who did not know about the baptism of the Holy Spirit, and Apollos had to have his knowledge completed by Priscilla and Aquila. Still others were only attracted to the power associated with the name of Jesus and wanted to misusing it outright, like Simon Magus and the seven sons of Sceva. And despite all this persecution, fragmentation, and confusion, the "conspiracy" held together.
In the middle of all this, Paul - already mentioned as one of the early persecutors of the church - miraculously converted to Christianity, and became one of its foremost evangelists, to the point of becoming one of the named witnesses in 1 Corinthians 15. He then got embroiled in the central controversy of the early Christian Church: how to handle the new Gentile believers. This controversy got so heated that Paul once had to publicly rebuke Peter for his stance, and James wrote his epistle with a vastly different emphasis from Paul on what it means to truly be a "believer". In other words, this controversy set all three of the named witnesses in 1 Corinthians 15 against one another, to some degree. And yet, the "conspiracy" endured.
And that's not the end to the divisions of the early church - A number of outright heretical groups had to be condemned - Paul pronounced anathema to a group proclaiming "a different gospel", and John pointed out certain "antichrists" at large in the world, and also named the works of the Nicolaitans as the objects of Jesus's hate. And despite all this division, the "conspiracy" remained.
Again, what kind of conspiracy does this? What conspiracy kills off its leader, fragments itself into dozens of different factions, bitterly fights itself on internal controversies, condemns some parts of itself, and still survives? And all for what purpose? Persecution, controversy, poverty, and death? That is all that any insider might have hoped to receive by adhering to their conspiracy. As Paul himself says in 1 Corinthians 15: "If in Christ we have hope in this life only, we are of all people most to be pitied."
If the "conspiracy" is that Jesus really did rise from the dead, and that this was the central truth that held early Christianity together, despite all of its divisions - then all this makes sense. But if you want all this to be the result of some made-up story, then you have to postulate a completely ridiculous conspiracy - one where the leaders somehow concocted the greatest and most effective lie the world had ever seen, despite being an inept, fractious group of people with little control over their followers. Or, you can instead postulate a truly vast conspiracy, one which planned for all this persecution and division and infighting from the beginning. You can postulate whatever you'd like. That's the whole appeal of conspiracy theories. But at the end, the prior odds for any conspiracy you postulate will be absolutely minuscule.
The "final" odds for the resurrection
All this is difficult to fully quantify in terms of a Bayes factor. But using the arguments about Paul's testimony from the earlier parts of this work, we know that his independence by itself is worth several orders of magnitude. Then the rest of the anti-crackpot properties can be used to simply firm up that value. Meaning, the overall Bayes factor of the entire anti-crackpot suite can be assigned, at a minimum, several orders of magnitude - let's say about 3 orders.
Recall that the Bayes factor for the resurrection ranged from 1e14 to 1e16, before considering the anti-crackpot defenses. Adding 3 more orders of magnitude results in 1e17 to 1e19. Against a prior of 1e-11, this results in a final odds of 1e6 to 1e8, as the conservative and likely values, respectively.
Here, I'm going to take off an order of magnitude for no reason other than an extra margin of safety. That gives us 1e5 to 1e7, and I would characterize this as "safely above 1e5". The odds for Christ's resurrection is safely above a hundred thousand to one, even after allowing the skeptic to consider every possible alternative explanations, up to and including all possible crackpot theories.
Furthermore, recall that this is still only using the data summarized in 1 Corinthians 15. We are still ignoring other important witnesses like the women at the tomb, and vastly underestimating the testimony of people like John.
But with those restrictions and conditions, "safely above 1e5" is my final answer for the odds of Christ's resurrection, for the purposes of this work. In other words, the probability that Jesus rose from the dead is safely above 99.999%.
Conclusion: the resurrection is still certain, even after taking every possibility into account
Let us summarize the "skeptic's distribution" argument for Christ's resurrection.
We've already seen that any kind of reasonable investigation into Jesus's resurrection accounts would conclusively demonstrate that Jesus did rise from the dead. The only possibility left for the skeptic is to turn to unreasonable hypotheses - that is, to crackpot theories like conspiracies.
The distinguishing feature of these theories is that they postulate a near-total interdependence among the evidence, as if they were all manufactured by a single source - the conspiracy. This allows them to ignore the abundance of evidence for a certain position, and instead attribute it all to a rather unlikely prior.
So then, how could we quantitatively consider the interdependence of evidence, fully taking everything into account, up to and including all the different possible crackpot theories?
We constructed the "skeptic's distribution" - the probability distribution for achieving a certain level of evidence for a resurrection, assuming a skeptical, anti-supernatural worldview. This probability distribution is actually quite accessible, since every single non-Christian resurrection report in world history would be the result of a sample drawn from it. And because it's constructed from these historical, empirical samples, the final distribution is quite indisputable - one cannot reject the distribution without rejecting history or empiricism.
Furthermore, such a distribution fully takes into account the aggregate of all the different types of theories that actually could have happened in history, including all the crackpot theories. The results of all things like conspiracy theories or religious mass delusions would show up in the samples, and the samples can then be extrapolated for things beyond what actually happened in history.
We also constructed the "Christian's distribution" for how much evidence might have been generated if Jesus really did rise from the dead. This distribution was broad and not very informative, because it was over a mostly counterfactual space of the different amounts of evidence that could have been generated from a true resurrection. But by calibrating against the evidence for historical figures known to have existed, we were able to get a specific functional form for this distribution. We furthermore tested this distribution against absolutely ludicrous limits, such as someone demanding a hundred times more evidence for the resurrection than what we actually have, and found that the distribution was very robust: even accommodating such absurd demands did not change the final results much.
Once we had the Christian's and skeptic's distributions, the rest was straightforward. The Bayes factor is simply their ratio at the x value corresponding to the amount of evidence we actually have, and we just applied this Bayes factor to the prior odds for the resurrection to get the posterior odds.
Initially we first constructed the "skeptic's distribution" using the most pro-skeptical assumptions possible. Even then, this gave even odds of Jesus's resurrection having taken place, under an impossibly favorable set of assumptions for skepticism. Re-running the calculation with demonstrably more realistic assumptions, which were still quite conservative, gave the posterior odds for the resurrection being somewhere between 1e3 to 1e5.
However, all of this considered only the sheer amount of testimonies for Jesus's resurrection. It did not consider the high degree of independence among these testimonies, which would further favor the case for the resurrection. For instance, just the conversion of Apostle Paul would be enough to put any kind of conspiracy theory beyond any realistic possibility. And Paul's independence only scratches the surface of the many defense against crackpot theories built in to the resurrection testimonies.
After taking these into account as well, and leaving some extra margin of safety, I gave the final odds for the resurrection as safely above 1e5. In other words, the probability that Jesus rose from the dead is safely above 99.999%, even after taking every alternative explanation - up to and including crackpot theories - into account.
All this was with only part of the evidence for Christ's resurrection - specifically those testimonies summarized in 1 Corinthians 15. A more complete look at all the testimonies would drive the numbers higher still.
The conclusion is clear: Jesus almost certainly rose from the dead.
The stance on non-Christian miracles
As before, we want to double check our methodology. We want to apply it to different situations and make sure that it gives the expected results.
A common argument from skeptics is that we cannot accept the miraculous stories about Jesus while simultaneously rejecting them for all non-Christian miracle-workers in world history. But that is nonsense. Of course we can discriminate between these stories: it just comes down to discerning which ones have enough evidence. We accept the ones that have enough, and reject the ones that do not.
So, for instance, we've already shown that the stories about Jesus's resurrection have far more evidence behind them than any other resurrection stories in world history. We've done the math. And that math, with its self-consistent logical rigor, compels us to both accept Jesus's resurrection, and reject the other resurrection accounts. It merely comes down to their respective level of evidence.
But what about other, non-resurrection miraculous stories? Could any such stories of non-Christian origins be true? A Christian must answer "no" for the most part. There may be some allowances for God sending 'rain on the righteous and the unrighteous', but certainly any miracles that expressly support a non-Christian worldview must be false.
And here, both Christians and skeptics can find common ground. We both believe that a large majority of non-Christian miracle stories must be false. And if the Bayesian methodology that I've employed thus far is sound, it ought to be able to come to that conclusion. And by doing so, that methodology will demonstrate its soundness - in accordance to Bayes' rule, for both Christians and skeptics.
So let's begin this extension into non-Christian, non-resurrection miracles, and thereby double check our methodology.
Ichadon
We'll start out with a quick, easy case, where the conclusion is not difficult to reach. Many miraculous stories fall into this category. A full-blown analysis is not necessary in such stories, as none of them reach anywhere near the level of evidence in Jesus's resurrection. Just a simple comparison with rough numbers to with our previous analysis will do.
For example, there's the story of Ichadon, an ancient Korean Buddhist monk. It's said that the miraculous signs accompanying his death resulted in the adoption of Buddhism as the state religion. His story is recorded in the "Lives of Eminent Korean Monks" - about 700 years after the fact. As we've mentioned before, this kind of time gap makes any kind of personal testimony impossible, so the level of evidence here only reaches a rather weak form of the "some people say..." level.
What is the Bayes factor for the "some people say..." level? As I previously argued, they must fall somewhere between 0.5 and 1 times the "once in human history" level. Given that there are probably at least hundreds of resurrection accounts with a "some people say..." level of evidence, and that they're likely to be more concentrated on the lower end of the spectrum, just because of the shape of the distribution, I'd say that about 1e6 is a good, generous guess for a typical "some people say..." level of evidence. A particularly weak version, like the one cited above for Ichadon, must have a still smaller Bayes' factor - maybe something like 1e5.
That's something, but it falls distinctly short of overcoming the small prior against a genuine miracle, which probably has a prior of at least 1e-8 against it.
Vespasian
Our first major case will be the stories of miraculous healing attributed to the Roman Emperor Vespasian. These are recorded in history through the following accounts:
Vespasian himself healed two persons, one having a withered hand, the other being blind, who had come to him because of a vision seen in dreams; he cured the one by stepping on his hand and the other by spitting upon his eyes.
- Cassius Dio, Roman History, 65.8
Vespasian as yet lacked prestige and a certain divinity, so to speak, since he was an unexpected and still new-made emperor; but these also were given him. A man of the people who was blind, and another who was lame, came to him together as he sat on the tribunal, begging for the help for their disorders which Serapis had promised in a dream; for the god declared that Vespasian would restore the eyes, if he would spit upon them, and give strength to the leg, if he would deign to touch it with his heel. Though he had hardly any faith that this could possibly succeed, and therefore shrank even from making the attempt, he was at last prevailed upon by his friends and tried both things in public before a large crowd; and with success. At this same time, by the direction of certain soothsayers, some vases of antique workmanship were dug up in a consecrated spot at Tegea in Arcadia and on them was an image very like Vespasian.
- Suetonius, The Lives of the Twelve Caesars: Divine Vespasian, 7.2
During the months while Vespasian was waiting at Alexandria for the regular season of the summer winds and a settled sea, many marvels continued to mark the favour of heaven and a certain partiality of the gods toward him. One of the common people of Alexandria, well known for his loss of sight, threw himself before Vespasian's knees, praying him with groans to cure his blindness, being so directed by the god Serapis, whom this most superstitious of nations worships before all others; and he besought the emperor to deign to moisten his cheeks and eyes with his spittle. Another, whose hand was useless, prompted by the same god, begged Caesar to step and trample on it. Vespasian at first ridiculed these appeals and treated them with scorn; then, when the men persisted, he began at one moment to fear the discredit of failure, at another to be inspired with hopes of success by the appeals of the suppliants and the flattery of his courtiers: finally, he directed the physicians to give their opinion as to whether such blindness and infirmity could be overcome by human aid. Their reply treated the two cases differently: they said that in the first the power of sight had not been completely eaten away and it would return if the obstacles were removed; in the other, the joints had slipped and become displaced, but they could be restored if a healing pressure were applied to them. Such perhaps was the wish of the gods, and it might be that the emperor had been chosen for this divine service; in any case, if a cure were obtained, the glory would be Caesar's, but in the event of failure, ridicule would fall only on the poor suppliants. So Vespasian, believing that his good fortune was capable of anything and that nothing was any longer incredible, with a smiling countenance, and amid intense excitement on the part of the bystanders, did as he was asked to do. The hand was instantly restored to use, and the day again shone for the blind man. Both facts are told by eye-witnesses even now when falsehood brings no reward.
- Tacitus, Histories, 4.81
So, what are we to make of these accounts?
We apply the methodology that we've been using all this time. How much evidence is there for these miracles? And is it enough to overcome the small prior?
None of the accounts give specific names for such individuals. We have some vague characters, such as "people of Alexandria" or "[Vespasian's'] friends" - but there are no named characters, except perhaps emperor Vespasian himself. However, this group of people seem to be well specified: they're better than the "some people" level of evidence that we've seen so much of thus far. The witnesses are the crowd of people who gathered in Alexandria and saw Vespasian heal these two people. Tacitus mentions eye-witnesses, and presumably he could have gotten to these specific individuals if he had to. So, overall, I would say that this testimony is on par with the 500 disciples witnessing Christ's resurrection. The Bayes factor for such a testimony can stretch in excess of 1e9, according to our previous calculations. It would be greater still if you counted Vespasian himself.
So, that's a pretty big Bayes factor, right? So this event actually happened?
But now we run into the problem of precisely defining what "this event" was. Did Vespasian "heal" two people in front of a large crowd? The prior odds for such an event is decently large - certainly much larger than someone coming back from the dead. Let's say, for the sake of argument, that it's around 1e-6. This is easily overpowered by the Bayes factor of the testimonies above, which exceeds 1e9 (although this value would be smaller if the prior were only 1e-6). We can be reasonably confident that such an event happened.
But was the healing supernatural? Now we're talking about an entirely different kind of event, with different prior odds. A supernatural healing of this type would be almost as unlikely as a resurrection. Since a resurrection had prior odds of 1e-11, let's be generous and assign this a prior odds of 1e-8. But... isn't the Bayes factor still large enough to overcome that?
No, not at all. For the Bayes factor itself now changes. For one, we can no longer count on Vespasian's testimony at all. Apart from the massive conflict of interest (to be addressed shortly), Vespasian himself doesn't believe that he can actually heal these people in the beginning. Tacitus explicitly reports that everything was perfectly achievable through mundane means, and that Vespasian only attempted the healings when he was informed of this possibility.
Therefore, Vespasian himself is certainly not testifying to anything like a supernatural healing here. Neither, for that matter, is the crowd itself, if things went according to what's in Tacitus's account. In fact Tacitus goes to some lengths to provide naturalistic explanations for the "healing" - to such a degree that his account should actually be counted as evidence against a supernatural healing. He calls these people "most superstitious", and nearly explicitly says that anyone in the crowd who actually believed in a supernatural healing would have been deceived. And there is nothing in either of the other two accounts to contradict his.
Tacitus's account is the earliest, most detailed, and most explicit in mentioning witnesses. The other two are mostly just summaries of his. And yet, in this best account, the idea of a supernatural healing is almost explicitly refuted. So what happens to the evidence? Where is the testimony?
There is essentially none left. At best it's reduced to that familiar, unspecific "some people say..." level. This is nowhere enough to overcome a prior odds of 1e-8, and therefore we can be very confident that a supernatural healing did not take place here.
In summary: on the question of whether there was a public spectacle where Vespasian "healed" two people, a prior odds of something like 1e-6 is overcome by a Bayes factor of around 1e9 - therefore we can reasonably hold that this actually took place. But on the question of whether this "healing" was supernatural, a prior odds of 1e-8 is not moved enough against a "some people say..." level of evidence, of around 1e5 or 1e6. We are therefore quite certain that the "healing" was not supernatural.
And all this is without taking into account the enormous potential for deception, conspiracy, political shenanigans, or a publicity stunt. Vespasian was a newly crowned Roman Emperor, after all. Taking that into account would lower the final probabilities even further, for both the supernatural and the mundane versions of the event. In the end, I think our methodology brings us to the point where there's better than even odds for some kind of public spectacle taking place, but the nature of the event was almost certainly not a supernatural healing.
Do you agree with that assessment? Does it seem reasonable to you? Good - then you are compelled to correspondingly increase your faith in the methodology we used, and therefore increase your degree of belief in Christ's resurrection.
"Something happened" vs. "a miracle happened":
But wait! Can a similar type of reasoning be used against Christ's resurrection? Could it be argued that "something" probably happened with a man we now call Jesus, but that it was not anything supernatural?
No, it cannot. The reasons that existed for Vespasian that allowed for such an argument simply does not exist for Christ's resurrection.
For one, a resurrection is nearly impossible to fake. One can fake being healed of blindness, or of a defective limb, without much effort. You can do it right now - you just need a little bit of acting skills. Just a bit of placebo effect or the excited anticipation of the crowd can be enough to get someone to walk around for a few steps, or convince a man with poor vision that he sees better. That is all that is required to generate the above accounts of Vespasian's miracles. But can you imagine making such an argument for a resurrection? "Are you sure that it wasn't just the placebo effect that cured his death? Or sometimes, if everyone in the crowd anticipates it, a corpse can be encouraged enough to get up and walk."
We believe that nothing supernatural took place in Vespasian's case, partly because what he achieved in healing is not all that remarkable. There are many possible naturalistic explanations. But in Christ's case, you need a naturalistic explanation for a man who was confirmed dead multiple times, who then came back walking, talking, eating, teaching, converting skeptics, and giving missions. Good luck getting all that with common naturalistic explanations like "placebo effect" or "crowd anticipation".
But secondly, and far more importantly, the evidence itself points towards a naturalistic explanation for Vespasian, and a supernatural event for Jesus. We are, as ever, evaluating and following the evidence. The evidence itself - in the form of Tacitus's account - spells out that Vespasian's miracles likely had naturalistic causes. In Jesus's case, it's again the evidence itself - in the form of the text of the New Testament - that consistently and repeatedly tells us that Jesus's resurrection was a supernatural event.
In order to draw an equivalence, and say that "something happened, but nothing supernatural" in both cases, you would need the same kind of evidence. You would need something like the Gospel of John explicitly stating that Jesus's disciples stole the body, and spelling out exactly how they did it and why there was nothing supernatural required. If the Gospel of John actually said such things, then you could draw an equivalence between the "miracles" of Vespasian and the resurrection of Jesus.
But, of course, the Gospel of John does not in fact say that. It is no good making up evidence you don't have. We are to only follow the evidence we actually have. So, merely mentioning that "something happened, but probably nothing supernatural" is worthless. It's wishful thinking about evidence you don't have. Speculations - merely mentioning possibilities - do absolutely nothing against a Bayesian argument. It is evidence, not speculations, that move probabilities.
So in considering all of the above, you see that the methodology is perfectly consistent in concluding that nothing supernatural happened in Vespasian's stories, while also concluding that Jesus rose from the dead.
Splitting the Moon
In Islam, the Quran itself is said to be Muhammad's chief miracle - but it is difficult to evaluate this claim. We would need to dig into specific passages in the Quran and interpret it, which would easily end up leading down a rabbit hole. Otherwise, it's hard to say that the mere existence of the text is miraculous. Rather, we want a clear miracle - a miracle that can be recognized as such by anyone, like a resurrection. That is the point of a sign, after all. What good is a sign if it can't be clearly recognized?
The best known Islamic miracle of that kind - a miracle which is clearly a miracle - is Muhammad's splitting of the moon. But even this miracle is highly controversial. There are even certain interpretations - Islamic ones - which deny that this took place at all. They say that it is rather a prophecy that's suppose to take place at a future time, or just an optical illusion.
The clearest case for the splitting of the moon being a literal miracle come from certain hadiths. Now, the sheer number of such citations and the authority they claim in going back to Muhammad's companions is indeed impressive - if one were to stop their investigation there.
But if you actually read these hadiths, you immediately notice how sparse they are. For example, one of the more detailed hadiths on the subject reads:
We were along with God's Messenger at Mina, that moon was split up into two. One of its parts was behind the mountain and the other one was on this side of the mountain. God's Messenger said to us: Bear witness to this.
And... that's it. Clearly, such a claim doesn't score particularly high on the "sincere and insistent" scale. Many of these hadiths are so short and free of context that it's hard to get a definitive narrative or interpretation out of them. For example, the above hadith is compatible with Muhammad (God's Messenger) causing the splitting of the moon, or with him merely pointing out some kind of a natural spectacle. In addition, many of these hadiths are highly interdependent, as their texts are often just a copy or a subset of one another. In fact, if you were to weave together all the independent text in all of the hadiths about this miracle, it would hardly amount to a decently sized paragraph.
Compare that to, say, the Holy Week narrative in the Gospel of John, which spans several chapters in length and leaves no ambiguity in relating Jesus's death and resurrection. The difference in narrative clarity and the level of detail is incomparable.
It is furthermore worth noting that these hadiths were generally written down over two hundred years after Muhammad's death. They claim a chain of transmission going back to some contemporaries of Muhammad, which is certainly something - this is what keeps the hadiths from degenerating to the "some people say..." level of evidence - but this chain often exceeds five or six people in length. These hadiths are therefore distinctly inferior to any of the testimonies in the New Testament in terms of their authenticity, just on this point alone.
Considering all this, it's hard to see how these sparse testimonies could add up to overcome the small prior odds for a miracle as remarkable as the moon splitting in two. Let's try a rough estimate: A full-blown, sincere personal claim of the type we've been studying has a Bayes factor of 1e8 or 1e9. But that's not what we have here. Instead, we have a set of short claims made with no context, relayed to us after more than 200 years, through a chain of transmission involving five or six people.
As I said, I consider this quite distinctly above the "some people say..." level of evidence. It may even reach or exceed the "once in world history" level, because I'm not aware of any other non-Muslim, non-Christian sources which document miraculous events in the manner of the hadiths.
On the other hand, these short passages, with very little contexts, and their highly interdependent texts, means that they cannot be really given any real consideration above the "once in world history" level. I'm fairly certain that I would rather have an extensive, detailed text by a single author giving a personal testimony, rather than a single paragraph chopped up and divided up among a group of 5 or so companions, which was transmitted along five or six people over 200 years.
These considerations put the Bayes factor of these hadiths at somewhere around 1e9 or 1e10, because it's around or better than the "once in world history" level, but no better or maybe worse than a single individual giving a detailed, insistent testimony.
Another way to think about this is to compare these hadiths more directly to the "some people say..." level of evidence. As the Muslims themselves say, "if not for the isnad (the line of transmission), whoever wanted could say whatever they wanted". In other words, the line of transmission is the only thing keeping the hadiths from falling into the "some people say..." level of evidence.
But really, how much evidence could the line of transmission add? Especially when it's over hundreds of years through several people? These are just a simple list, amounting to less text than the messages themselves. Surely, that's something, but it's hard to imagine that it's worth more than several orders of magnitude. This line of thinking also gives numbers like 1e9 for the overall Bayes factor of the hadiths.
Yet another way to think about this is to consider these hadiths to be parallel to the testimony of the group of apostles mentioned in 1 Corinthians 15, if we only had very sparse records of the apostles from over two hundred years after the fact. This again brings us to numbers less than 1e10.
So no matter how one slices it, the Bayes factor of the hadiths amount to less than 1e10. This is even before considering the fact that the hadiths may not really even be claiming that Mohammed split the moon as a supernatural event.
On the other hand, a miracle like splitting the moon is indeed highly remarkable - so it should at least be given a prior odds on par with the resurrection, of 1e-11. So the math doesn't work out. The evidence just doesn't add up. A Bayes factor of less than 1e10 doesn't overcome a prior odds of 1e-11. In addition, we must consider that there are no credible non-Islamic records of this highly visible and remarkable astronomical event, and the fact that there are good Islamic reasons to disbelieve that this ever happened. At the end of it all, we can be fairly confident that this did not actually happen as a miracle.
So, overall, we can say that our methodology does correctly reject non-Christian miracles. This validates the methodology for our test cases, and therefore compels us to accept the results when the same methodology says that Jesus definitively rose from the dead.
Accounts in Josephus
Let us now consider some miraculous stories from the works of Josephus.
Josephus was a Jewish historian who was active in the latter half of the first century. His works include The Jewish War and Antiquities of the Jews. They deal with the contemporary and the ancient history of the Jews, from the perspective of the a Jew living after the Siege of Jerusalem and the destruction of the Second Temple in 70 AD.
As such, he is a valuable resource in understanding the background of early Christianity, and his works are quite compatible with the New Testament. The miracles recorded his works that we're about study are likewise Jewish in origin, and compatible with Christianity. It would do Christianity no harm if these miracles really took place. They do not meet our earlier criteria of "miracles that expressly support a non-Christian worldview". In fact, Christianity could quite happily accommodate Josephus's stories about the signs surrounding the sacking of Jerusalem (Jewish War, 6.5.3).
After all, Christianity started out as a Jewish sect, and acknowledges the fundamental truth in Judaism. Jesus himself was Jewish, and famously predicted the sacking of Jerusalem. The New Testament acknowledges the existence of miracle workers and exorcists outside the immediate circle of New Testament Christians, of varying degrees of legitimacy, including one that Jesus himself was okay with.
However, even all that doesn't mean that we ought to uncritically accept the miraculous stories in Josephus. We will evaluate some of them, according to the methodology we've developed, and thereby also evaluate the methodology itself.
Now there was one, whose name was Onias, a righteous man he was, and beloved of God, who, in a certain drought, had prayed to God to put an end to the intense heat, and whose prayers God had heard, and had sent them rain.
The rest of the story is about how a warring faction attempted to get him to use his miraculous powers against their enemies - so apparently his feat was publicly known. He is also mentioned in some other Jewish works, where his story is told in a little more detail.
Now, what are we to make of this story? Unfortunately Josephus doesn't mention any specific sources in relating this story. He simply tells it as a story, more than a hundred years after the fact. That means we don't have anything like any of the direct witnesses we have for Christ's resurrection. The other sources are similarly dated, although dating exact passages in the Talmud is tricky. The best we can do here is infer that Josephus and others must have heard the story from someone, presumably from a group of people. But given that we don't know much else, again the most we can do is credit this account with the "some people say..." level of evidence.
Now, this is a fairly strong case of the "some people say..." level of evidence, because of its multiple attestation, and parts of the story being placed in a definite historical setting. But overall, this type of testimony is not enough to overcome the small prior against a supernatural event - I'd judge the numbers here to be something like a prior of 1e-9 against a Bayes factor of 1e7 - and we must judge that this event did not actually occur as a miracle.
Of course, if you have some other, prior reason to believe in the existence of the God of Israel - say, because of Jesus's resurrection - then that may be enough to push this event over the top. So it could be acceptable for someone who is already a Christian to find this account convincing. But leaving aside this complication, and looking just at the records about Honi in isolation, the evidence provided falls short of overcoming the prior.
Next, let us consider the story of Eleazar the exorcist, as told in the Antiquities of the Jews, 8.2.5:
I have seen a certain man of my own country, whose name was Eleazar, releasing people that were demoniacal in the presence of Vespasian, and his sons, and his captains, and the whole multitude of his soldiers. The manner of the cure was this: He put a ring that had a Foot of one of those sorts mentioned by Solomon to the nostrils of the demoniac, after which he drew out the demon through his nostrils; and when the man fell down immediately, he abjured him to return into him no more, making still mention of Solomon, and reciting the incantations which he composed. And when Eleazar would persuade and demonstrate to the spectators that he had such a power, he set a little way off a cup or basin full of water, and commanded the demon, as he went out of the man, to overturn it, and thereby to let the spectators know that he had left the man; and when this was done, the skill and wisdom of Solomon was shown very manifestly: for which reason it is, that all men may know the vastness of Solomon's abilities, and how he was beloved of God, and that the extraordinary virtues of every kind with which this king was endowed may not be unknown to any people under the sun for this reason, I say, it is that we have proceeded to speak so largely of these matters.
Well, now this sounds pretty impressive! Josephus names himself as an eyewitness! And also his Roman patron, the emperor Vespasian, whom Josephus would not invoke lightly! And a great number of Vespasian's associates! Let's see what we can make of this.
First, Josephus and Vespasian are both very well known historical characters, easily on par with the named individual witnesses in 1 Corinthian 15. Josephus furthermore mentions a crowd of other people - Vespasian's sons, captains, and soldiers. This crowd is specific enough to match the crowd of 500 in 1 Corinthians 15. The only thing missing from the roster in 1 Corinthians 15 is the group of apostles, and a third major historical character. So that's nearly as much evidence as there is for Christ's resurrection, right?
But we have not yet considered the full qualifications to match the 1 Corinthian 15 witnesses. First, Josephus's testimony here is nowhere as earnest or insistent as the testimonies of someone like apostle Paul. The above passage is the only thing that's known about this Eleazar. Josephus mentions him this one time, and that's it. Compare that to the twelve disciples, who completely oriented their entire lives around the resurrection of Jesus Christ. Compare also to the apostle Paul, whose every writing can be traced back to his testimony that Jesus rose from the dead. There can really be no comparison.
Furthermore, it's worth noting that Josephus mentions this story in a larger narrative about king Solomon. Yes, that Solomon - the son of king David, builder of the first temple, well known for his wisdom. What's a story involving Vespasian doing in a narrative about king Solomon, who lived a thousand years earlier? Well, it turns out that this whole story is actually an aside, an anecdote that Josephus tells to demonstrate how wise Solomon was. He was saying that Solomon was so wise that his wisdom was used to exorcise demons even after all this time. In other words, the whole story is a parenthetical remark to the main point he was trying to make. In fact, for Josephus's main point, it doesn't even matter if this exorcist was genuinely supernatural. A fake exorcist invoking Solomon is still evidence for Solomon's renown. This erodes the testimony further on the "earnest" and "insistent" scales, for everyone involved.
In addition, there's an overwhelming amount of dependency factors at work here. Josephus's main motive, as plainly written out in the text itself, is to impress his Roman audience with the wisdom of Solomon. And this motive drives - and therefore serves as the source of dependency for - his choice to name the other witnesses in his account, and describe the exorcism as a success. Given that he was writing to a Roman audience about Solomon, one of the most famous Jewish kings, it makes sense that he would invoke Vespasian and his associates.
But it's important to note that we're not told what Vespasian and his associates thought of the whole affair. Indeed it's not even clear that they can be said to have given any testimony. Josephus mentions that they were in the audience, but he does not record their personal reactions. Clearly they cannot count as being more impressed than Josephus, as there are no records of any testimony that they, or anyone else, gave concerning this event.
And this complete lack of any other mention of this story makes the dependency factors far worse. The testimonies in 1 Corinthians 15 are of course all attested to in multiple other places in the New Testament, and corroborated by multiple non-biblical sources. We have no doubt that their testimonies are accurately summarized in 1 Corinthians 15. Even Vespasian's healing miracles had multiple attestations. But with this story, it's Josephus and only Josephus, who is himself one of the named witnesses. Everything depends on his testimony, on that short passage he wrote - including his claim that there were other testimonies. This dramatically increases the chance of near-complete dependency among the witnesses.
Lastly, it's again worth noting that a resurrection is nearly impossible to fake, whereas in Josephus's story the text itself suggests that nothing remarkable happened. He specifies very simple, physical things involved in the exorcism: a ring was put up to the demoniac's nostril. The man fell down. There were incantations mentioning Solomon. A container of water was knocked over. All these are simple, ordinary, non-supernatural events. There is no mention of whether the man was actually restored, in the sense of being in his right mind, free of demonic influence. Taken altogether, it again looks like nothing much happened, and this is far less remarkable than the resurrection of a man who was confirmed to be dead multiple times, who then came back walking and talking.
So we see that while the roster of witnesses is pretty impressive for Eleazar's exorcism, their testimony is actually very weak in comparison to their parallels in 1 Corinthian 15, according to our previously established rules for matching testimonies.
"Something happened" vs. "a miracle happened", again
So, let's consider two separate versions of what happened, as we did for Vespasian's healing miracles. First, did something remarkable happen with Eleazar performing in front of a crowd? And second, was it an actual, supernatural exorcism of an actual demon?
As with Vespasian's healing, let's give the first, non-supernatural "something happened" version of the event a prior odds of 1e-6. On the evidence side, after taking everything above into account, I'd give Josephus's testimony for himself a Bayes factor of 1e5 - about half as strong as a full-blown, earnest, insistent testimony. Vespasian's testimony must be significantly less than this, because of the very strong dependency factors involved. It is entirely dependent on Josephus's testimony, and Josephus has a strong motivation to mention Vespasian in appealing to a Roman audience in telling a Jewish story. I'd give Vespasian a Bayes factor of around 1e2, and his associates 1e1. That all comes to a combined Bayes factor of 1e8.
Or, perhaps a better way of thinking about this is to say that we really only have Josephus's testimony, but the fact that he's willing to involve Vespasian shows that he's quite serious, and that upgrades his testimony to make it earnest, giving it a Bayes factor of 1e8. In the end, this very rough calculation comes out to about a final odds of about 1e2. We can be fairly certain that "something happened" here.
As for the "actually supernatural exorcism" case, we'll again start with a prior of 1e-8, as in Vespasian's healing miracles. As for the Bayes factors, Josephus himself gets 1e4. He clearly tells the story as an exorcism which he himself witnessed, but his focus on the physical aspects of the story sounds like he has some doubts himself as to whether there was actually anything spiritual going on - so he loses an order of magnitude compared to the "something happened" case above. Vespasian and his associates together get 1e1. The drop here for them is due to the lack of any testimony concerning what they thought about the event. Overall, the combined Bayes factor is 1e5.
Again, we can think of this as being entirely up to the testimony of Josephus - he starts with a Bayes factor of 1e8 as in the "something happened" case, but loses 3 orders of magnitude because of the relative ease of faking this kind of exorcism, and his lack of any mention of how Vespasian and his associates reacted. So then, this Bayes factor of 1e5 is set against a generous prior of 1e-8, resulting in a final odds of 1e-3. Therefore, we can disbelieve that anything actually supernatural happened in the story, with some confidence.
The calculations here are quite rough, but I'm fairly certain that the results here are good to a couple orders of magnitude. Something probably happened, but nothing supernatural. Again, does that sound reasonable? Is that what you would have concluded upon reading this passage from Josephus? Good - then the methodology we used is further validated, and the resurrection of Christ is therefore made more certain.
Double checking with a rule of thumb
The double checks in the previous chapter have been only for the strength of a human testimony. We have not yet explicitly tested the methodology of comparing the "skeptic's distribution" with the "Christian's distribution". And you'd be right in wanting to test this methodology: it's fairly complicated, involves a decent amount of math, and it uses a computer program in a key step to calculate the Bayes factor. Perhaps there's a mistake in the math, or a bug in the code?
But because of complexity of the method, it's also hard to test it exactly as it is. It would be difficult to find a natural experiment which matches up exactly with the circumstances surrounding Christianity, to which we could apply our exact method. Therefore, I instead propose testing a simpler rule of thumb. This rule of thumb will include less stringent conditions than the full "ratio of distributions" methodology, and therefore it will, once again, serve as a lower bound on the strength of the pro-resurrection conclusions that the full version can reach.
Here's the rule of thumb: in any category of human behavior, for any numerically non-negative primary measure of that behavior, the ratio between the maximum and the second-to-maximum values will be less than a factor of 6, for a sufficiently large and inclusive population.
Now, here's how this factor-of-6 rule applies to the argument for Jesus's resurrection: consider all the human deaths in history. Under the assumptions of naturalism - that is, assuming that there was no real resurrection for any of these people - these deaths will still generate some amount of evidence for a resurrection afterwards. Of course, this amount will be zero in most cases, but there will be some rare cases with distinctly nonzero evidence. The factor-of-6 rule says that, for such a set of resurrection evidence, even for the most extreme, "once in world history" case, the maximum amount of evidence SHOULD be within a factor of 6 of the runner-up.
Of course, this DOESN'T work for Jesus's case. The level of evidence for his resurrection is far greater than 6 times the runner-up. The only possible explanation, according to our rule of thumb, is that the initial assumptions was violated: this level of evidence was not naturalistically generated, because Jesus did really come back from the dead.
Now, this is just a rule of thumb. It's far from the complete methodology we used in our "ratio of distributions". We aren't constructing any distributions, and we're completely ignoring the number of "outliers". We therefore expect the conclusion we reached above to be a lower bound on what's possible from the complete methodology. So validating this rule of thumb will serve as a sufficient double check on the complete methodology.
Of course, it still remains for us to actually validate this rule. We want to show that it works very reliably, not just for the resurrection, but for any primary metric covering any category of human behavior, regardless of any possible dependence factors. Note that we won't require it to work in absolutely every case, for two reasons: one is that our argument is probabilistic by nature, and the second is that the rule is just a rule of thumb, derived by relaxing the conditions from a more rigorous methodology. So we should not be surprised if we find a rare exception. But we still need to establish that the rule works reliably, in a great majority of diverse cases.
If we can establish that, we can use it to argue for the resurrection as we have just few paragraphs before. Then the full "ratio of distributions" approach would be just putting more stringent conditions on our data, which allows us to quantify and firm up our conclusion.
Richest people in the world
For our first example, let us again look at the richest people in the world, whom we've considered before. There is perhaps no example that comes to mind more readily when we speak of dependency factors in human behavior: the rich get richer. Money begets money. It's quite difficult for an average person to earn a billion dollars: Jeff Bezos might literally do it in his sleep on any given night, just from the random fluctuations of the stock market.
Given this extreme dependence factor of needing money to making money, you'd perhaps think that individual wealth could generate outliers such that the richest person might be many more times wealthier than the runner-up. But empirically, this does not bear out. Even the extreme kind of dependencies in wealth generation doesn't allow for such a maximum value.
Wikipedia's page on the richest people in the world shows that, at the time of this writing, the gap between the richest person in the world (the aforementioned Jeff Bezos) and the runner up (Bill Gates) is only a factor of 1.5 - far short of the factor of 6 we posed as the limit. Furthermore, we come no closer to the limit when we consider the wealthiest figures in history - the corresponding Wikipedia article has only a factor of 1.2 or so between the richest (Jakob Fugger) and the runner-up (John Rockefeller).
However, if you wade into murkier data, you may find people saying things like "Augustus Caesar was worth $4.6 trillion dollars". Doesn't that break the factor-of-6 rule, compared to people like Jeff Bezos or Jakob Fugger? It does, but only in a way that more firmly establishes the rule - for you see, we're now in a different category altogether. When we bring up people like Augustus Caesar, we're no longer discussing the wealth of private individuals, but the net wealth of a country ruled by an autocrat. So, apart from the fact that wealth attributed to rulers of entire empires are quite nebulous, their existence only serves to further enforce the factor-of-6 rule: that when it is broken, we're in a different category altogether. In the same way, when this rule is broken for the amount of evidence for Jesus's resurrection, this requires a change in category - from "naturalistically generated evidence" to "supernaturally generated evidence".
Of course, you may be prompted by examples like Augustus Caesar to look into the rulers of the largest empires that existed in history - perhaps there may be an example there which breaks the factor-of-6 rule? Well, here's the Wikipedia page for the largest empires in history - again, whether you sort by population, land area, or population density, the difference between first place and the runner-up only reaches about a factor of 1.5. So the factor-of-6 rule is further established, even in the cases of political power wielded by emperors.
Sports records
The world of sports is an excellent source for the kind of of data we're looking for. Many people try some kind of sports to some degree as they grow up. Those who have the talent and drive to perform well become a self-selecting group, who then become surrounded by personal and structural encouragements to further pursue their sport. This positive feedback loop repeats at every level of competition as they get better and better, driving them towards more practice, better coaches and equipment, and higher incentives to succeed. So at the highest levels, an athlete's primary metrics - especially their career-spanning metrics - display exactly the kind of highly dependent, human-based distribution we're looking for: LeBron James has a much higher chance of scoring another NBA basket than me, because the chances of you scoring a basket strongly depends on how many you've already scored.
With this perspective, let's look at some records.
Wayne Gretzky is widely held to be the greatest hockey player ever. He scored 894 goals and has 1963 assists, which puts him at first place for both of these categories. But do these records break the factor-of-6 rule? Not remotely: the numbers of the runner-up in each of these categories is 801 goals and 1249 assists. Again, the ratio between first place and the runner-up is limited to a factor of about 1.5.
What about records in soccer? Looking at the list of men with the highest number of goals, we find much of the same story - the ratio between the first place and runner-up amounts to less than 1.1.
Let's go back to basketball, and try as hard as we can to break the system. Dennis Rodman was a great basketball player, and skepticalsports.com does an excellent job of making the case for his value. In the process, the author generates this graph to illustrate just how good Rodman was - and reminds you to think "Holy Crap!" in response. It is indeed a remarkable graph. It plots a player's win differential divided by his possession usage rate (see the linked page for more details on what that means), for a variety of NBA players. Now, this statistic breaks our rule of requiring a "primary measure": win differential / usage rate is a complicated, non-standard measure, and it's picked out as the measure which best showcases Rodman's exceptional impact. And yet, even in this "Holy Crap!" graph, which we've allowed despite it breaking the "primary measure" rule, the ratio between the highest value and the runner-up is only about a factor of 2. Our factor-of-6 rule remains untouched.
How about if we look at sports more broadly? Consider the Olympic Games. The individual with the greatest number of Olympic medals is American swimmer Michael Phelps, with 28 total medals, 23 of them gold. The runner-up is Soviet Gymnast Larisa Latynina, with 18 total medals, 9 of them gold. Whether you compare total medals or gold medals, the ratio between the first place and the runner-up hardly goes over a factor of 2.
To be sure, there's many more sports statistics that we can look at, and perhaps there are some rare exceptions that we have yet to uncover. But the overall conclusion will not change: as a rule of thumb, the factor-of-6 rule is firmly established in the wide world of sports records.
YouTube, Instagram, Twitter
There are certainly strong dependence factors in wealth generation or sports records. But perhaps an even better example of human dependency factors would be today's internet culture, where so much depends on certain "memes" going "viral" to "break the internet". Indeed the internet is the cultural incubator which gave rise to all of these terms, where causing such an event is the goal of so much of its users and content.
It's instructive to do a side-by-side comparison of the dependence factors involved in the two sides we're considering. On one side, we have the evidence of Jesus's resurrection reports. For the other side, let's consider the number of views that the most popular videos get on YouTube.
So, you think there might have been a group of conspirators behind the evidence for Jesus's resurrection? Well, perhaps. But for YouTube, you don't have to speculate: their most popular videos are highly polished music videos, and we know for certain that there are huge teams of talented and well-paid professionals working full-time to make sure that the video is as well-produced and popular as possible. They have dedicated publicists, scores of beautiful models, technically proficient film crews, top-tier makeup artists and choreographers, and of course, some of the most famous singers and musicians in the world. There is no question as to which side would have stronger dependence factors in terms of their intrinsic "production value".
How about spreading and popularizing the idea? You think that Jesus's resurrection story could have easily spread far and wide from repeated oral tellings in the early Christian community, through preaching sermons and travelling missionaries? Well, whatever the medium of propagation was, it was certainly slower and less convenient than today's internet, where a video can be viewed with just a click at any time, from anywhere around the world. Again, there is no question that YouTube videos enjoy a huge advantage in their ease of propagation.
What about official, structural, or systematic support for the spread? Well, Christianity started out by its leader being executed as a lowly criminal by the most powerful government in the world. Then his remaining followers went around saying "no, really, you should still join us". As expected, they were persecuted right from the beginning, with few other movements in history facing more structural or systematic disenfranchisement.
YouTube, on the other hand, is one of the most popular platforms on the internet, backed by one of the largest and most powerful companies in existence. Some of the smartest people in the world are working constantly to make sure that their system is stable, inviting, and addictive. Their most popular videos are easy to find and likely to rapidly acquire new views, since it's to YouTube's interest to further push such videos and put them out in front of more people. Again, in terms of systematic support, the popular videos on YouTube win, hands down.
All these factors suggest that the dependence factors for videos "going viral" on YouTube must be absolutely enormous - certainly much larger than news propagation in the ancient Roman Empire. The popular videos therefore must end up with a truly staggering number of views, and the most popular must be miles ahead of the rest, even to the point of maybe breaking the factor-of-6 rule, right?
Here are the results. At the point of this writing, the most popular video on YouTube is Despacito, with 6.26 billion views - less than 1.5 times greater than the runner-up at 2.25 billion views. Even with nearly every conceivable advantage that our modern world can throw at it - with the best content placed on the most facile communication network dedicated to making things go viral - YouTube videos don't come anywhere near breaking the factor-of-6 rule.
If that wasn't enough, this has always been true throughout YouTube's history. You can look through the history of the highest viewed YouTube videos page on Wikipedia, but perhaps an easier source to digest is this video. Even when we look at video views on YouTube since near its founding, we hardly find any cases where the factor between the most-viewed and the runner-up is much greater than 2.
The story is much the same for other metrics of internet popularity. The lists of most-subscribed YouTube channels, most-followed Instagram accounts, and most-followed Twitter accounts all show less than a 2:1 ratio between the most popular accounts and the runner-up. And that's without even excluding the @instagram account on Instagram itself, which is obviously a special case.
Again, no matter how you cut it, our factor-of-6 rule is solidly validated.
Greatest number of marriages
Perhaps you want something with a connection to how Jesus generated his incredible statistic? What kind of mechanism was at work there? How did he get so many people to testify to his resurrection? Well, the foundation of Jesus's work among his disciples was intense, personal connections: he possessed extraordinary charisma of some kind, and somehow inspired incredible loyalty among his followers. This is how he managed to start Christianity, in only about three years - despite leaving no writings, and having no financial, military, or political power of any kind. It was all done with personal relationships.
What kind of statistics can we look to which would capture this idea of personal connections? A marriage would qualify. Here, let us restrict ourselves to the number of legally recognized monogamous marriages - if we consider polygamous marriages, or the total number of sexual partners, we would rapidly run into scenarios where we get away from the idea of personal connections. A dictator or an emperor may simply acquire partners as a measure of their political power, and for a sex worker the number of partners is simply a function of their daily grind. The record numbers in such cases quickly balloon up beyond anything that can be considered as personal connections. In any case, they would have no chance of braking the factor-of-6 rule, as they're capped by a human's biological limits.
So, who's the person that's been married the most number of times? Wikipedia tells us that it's Glynn Wolfe, who was a part of 29 monogamous marriages. I couldn't find the number for the runner-up, but the same article tells us that one of his wives (Linda Wolfe, née Essex) is the record holder for the most-married woman, with 23 marriages. So at best the ratio of the maximum to the runner-up is 29 to 23, which is nowhere near a factor of 6.
Factor-of-6-rule: conclusion
That's plenty of examples, from a broad range of human behavior. The factor-of-6 rule is firmly established. None of the other cases came anywhere near breaking it, with most examples hovering around a factor of 1.5 or so between the maximum value and the runner-up. Few examples reached past a factor of 2.
I must mention that there is no conscious selection bias in my examples above. They are simply the first fitting examples which occurred to me. Any examples I rejected were due to a lack of available numbers, or a violation of the conditions in the factor-of-6 rule. There were no examples which I rejected because I did not like the result.
Furthermore, I must again mention that finding a couple of hand-picked counterexamples would be insufficient to disprove our rule. The factor-of-6 rule is a rule of thumb: we do not need for it to hold in every case without exception. We only require that it serve as a good general guideline, which it clearly does. This is enough to serve as a double check on our original methodology, where we compared the "skeptic's distribution" with the "Christian's distribution", using greater rigor and more stringent conditions.
What, then, would invalidate our double check? You would need to show that the factor-of-6 rule failed, as a rule of thumb: if you could find, say, a dozen examples, which were not cherry-picked, across a broad range of human behavior, which all fit the conditions in the factor-of-6 rule, and yet smashed through that upper bound of 6 by a large margin, then that would do it.
Failing that, our conclusion is inevitable: Jesus must have really risen from the dead, because naturalistic explanations cannot generate the amount of evidence that Jesus has for his resurrection, which is more than 6 times that of the naturalistic runner-up. As a rule of thumb, such factor-of-6 extremes cannot exist in any measure of positive human metrics, even if they involve very strong dependence factors.
This is, by itself, sufficient to firmly conclude that Jesus rose from the dead. But remember that this is only a double check on our earlier real argument, which explicitly compared the ratio of the "skeptic's distribution" to the "Christian's distribution" to find the Bayes factor. This double-checked "ratio of distributions" method is now that much more certain, and its conclusion is beyond any reasonable doubt: Jesus almost certainly rose from the dead.
(ufo sightings, living in a simulation, a case that works out?)
Double checks: conclusion
So, all that covers the numerous ways to test our methodologies. It has passed them all. In everything there is perfect logical consistency and harmony. We believe all the things that ought to be believed, and reject all the things that ought to be rejected. And our methodologies, which passes all the tests of the skeptics and the other religions, clearly concludes that Jesus Christ almost certainly rose from the dead.
The rationale for this challenge
Is anyone still skeptical of the fact that Jesus rose from the dead? Well then, here is one more test, straight from a hallmark of the scientific method:
If you think that the evidence for Christ's resurrection was naturalistically produced, then replicate its results.
We have seen that history, in its natural course thus far, has utterly failed to reproduce a Jesus-level of evidence for a resurrection. It has not even come remotely close. And this has not been for a lack of trying, either - we've cited multiple cases where people tell a resurrection story, but their level of evidence always fell incomparably short of Christ's resurrection.
But perhaps you might succeed! And really, there isn't any fundamental reason why you can't, if indeed Christianity started naturalistically. In fact, if you are not convinced by the arguments in this work, a scientific mindset demands that you give it a try.
So, do you think that there was a massive conspiracy among the disciples to steal Jesus's body and start a new religion? Well, try to start a similar conspiracy of your own! See how well it holds up over the years when people rightly accuse you of being liars, and rightly threaten your reputation and wealth - perhaps even your life and limb!
You think that the Christian resurrection stories started through a mass hallucination, caused by eating a psychoactive plant native to Jerusalem? Well, go find that plant, feed it to a bunch of people, and see if they have the exact same hallucinations about the resurrection of one single person!
You think that some gullible religious people couldn't learn to cope with the death of their charismatic leader, and therefore made up the resurrection story? Well, start such a religion yourself, pretend to die, and see what happens!
Don't complain about the scope of the problem, or the amount of people, time, or money you need. Jesus started Christianity with just a handful of his disciples, in just about three years. You and your circle of friends could easily out-scope this group. This is not an experiment that's too big to be attempted. In fact, real-world, large-scale studies on health or sociology regularly out-scope the humble beginning of Christianity.
Don't complain about the right combination of social circumstances needed for Christianity to take off. If you can read this, you probably have access to world-wide travel and possible exposure to an enormous variety of the world's cultures - an advantage that Jesus's disciples did not have. You think that the right set of circumstances only exist in one particular tribal group in Papua New Guinea, or in a specific small town near the outskirt suburbs of Kyoto? You can actually travel to these places, and access the right social and cultural circumstances.
I am being serious here. This is not some cheap taunts against skeptics. If you've read my other writings - if you've even just read everything I've written above - you know that I welcome the testing of my ideas, and that I'm ready to change my beliefs as a result. If you really do come up with a plausible, naturalistic, reproducible way for Jesus's resurrection reports to have been generated, I will change my mind.
But remember that this works the other way too. We've already seen that the failures of the non-Christian resurrection stories have only made Jesus's resurrection more certain. In the same way, failure to replicate Jesus's resurrection reports must, of logical necessity, change your mind. You must become more certain of Christ's resurrection.
Of course, abject failure is in fact the most likely outcome of such an experiment. The experiment will produce something - but that something is not likely to be any better than the many other examples in world history, where a "resurrection" was said to have occurred. It will fall pathetically short of the level of evidence established by Christ's resurrection.
And that is why I, personally, won't conduct this experiment: I think the result will be negative - that it will not really add anything new to the data we already have. Furthermore, I have already done my due diligence, and am already well convinced that Jesus rose from the dead. This only cements my expectation of a negative result. I therefore have little reason to conduct this experiment, no more than I have a reason to reproduce the Michelson-Morley experiment to search for the luminiferous aether - I would rather believe in special relativity.
But the situation is exactly the opposite for a skeptic: they should expect a positive result, that there actually is a way to naturalistically reproduce Jesus's resurrection reports. This would, furthermore, be a new result with high impact, which overturns all the historical accounts thus far. They therefore have every reason to conduct this experiment - just as Michelson and Morley did for their famous experiment.
So, that is the challenge: if you are a skeptic, you have every reason - including scientific obligation - to try to replicate Jesus's resurrection reports, to achieve the same level of evidence. Failing the challenge - even just refusing the challenge - will have its own consequences, concerning your rationality or your actual beliefs.
The conditions for the challenge
So then, what would count as replicating the evidence for Christ's resurrection?
It's simple. The replication would be a new religious movement based on a "resurrection", which must match or exceed all of the essential components of the original evidence for Christ's resurrection. These components are merely what we've been discussing throughout this work, and they consist of the following:
First, the replicated "resurrection" must have sufficient evidence in terms of personal testimonies. These must be enough to match or exceed the set of six testimonies summarized in 1 Corinthians 15, with the following "matching" conditions:
To match Peter, James, or Paul's testimonies, we will require a report of a sincere, insistent, and enduring personal testimony given by a single named individual. This person must have been a public figure whose entire life (choice of profession, place of residence, etc.) was lived in complete alignment with that testimony. History must be able to locate this person with great precision, and have a good amount of information available about them.
To match the testimony of "the twelve", we will require a report of a sincere, insistent, and enduring personal testimony by a group of about a dozen named individuals. They must have been public figures whose entire lives were lived in complete alignment with that testimony. History must be able to locate these people with good precision, and have a good amount of information on at least some of them.
To match the testimony of the other apostles beyond the twelve, we will require a report of a sincere, insistent, and enduring personal testimony by a group of individuals. At least some of them must be named. At least some of them must have been public figures on the matter of their testimony. History must be able to locate some of these people with good precision, but not a lot of historical data is required of them.
To match the testimony of "the 500", we will require a report of a sincere personal testimony by a large crowd of people. They need not be named, or be public figures, or endure in their testimony, or have any additional information known about them. But history must be able to locate these people precisely enough, so that at least some of them could be theoretically pointed out individually by a well-known figure like Apostle Paul.
The report of each of these personal testimonies must be publicly accessible, reasonably corroborated by multiple sources, and approved by the continuing community surrounding the resurrection event.
Next, this evidence for the replicated "resurrection" must have the certain qualities which make conspiracies and other crackpot theories unlikely. Again, this is only what we've covered before - but here it takes on added importance, since we're specifically talking about artificially replicating the evidence.
One of the prominent, public witnesses must be someone who was publicly known for being strongly opposed to this new "resurrection" movement from the beginning. This person must have done real, material, significant, and public harm to that movement, prior to his or her change of heart. That change of heart must come from a conviction that this "resurrection" really happened.
There must not be an obvious prior connection or common cause among the prominent, public witnesses. They must be reasonably independent.
Within, say, 50 years of its beginning, this "resurrection" movement must cover a wide geographical area with great cultural and linguistic diversity - an appropriate region might be "the Middle East", "the Mediterranean", or "Southeast Asia". Its numerous followers, too, must reflect this diversity. As a corollary, the movement cannot be entirely directed by a central authority, and different parts of it must be in severe contention with one another, despite them all being in agreement about the "resurrection".
The major witnesses must be "sincere, insistent, and enduring" for those 50 years. They must staunchly testify to the replicated "resurrection" for at least that long.
Material wealth or political power cannot be a tangible, or even likely, reward for joining the movement.
There must be no evidence against this "resurrection" which endures past the 50 year mark.
Third, there are some further implicit factors which now need to be spelled out.
This movement cannot be built on Christianity. Otherwise, the strong dependency factors would ruin the experiment. It must achieve everything from scratch, without a preexisting foundation guiding how things ought be or ought to turn out - just as Christianity itself did. It's okay for the movement to get started in a "Christian nation", it just can't be directly based on or inspired by Christianity.
The entire replication must be plausible. After all, your attempt has some tiny chance to match the above conditions due to pure chance, but we must protect against such an occurrence counting as a genuine success. So, if you successfully start such resurrection-based movement, but it requires circumstances which occur once in a trillion years, that would not be considered plausible. For example, let's say you find a reproducible way to convince people of a "resurrection". But it only works on quintuplets who were struck by a ball lightning at the moment of their conception, and it can furthermore only take place when twelve comets brighter than Venus simultaneously show up in the night sky. Such an explanation for the original, Christian resurrection is not plausible, even if it may be naturalistic. Whatever mechanism you use to generate your replication must be likely enough to have had a decent chance of actually occurring in history.
Lastly, you may not brute force the problem with an overwhelming amount of resources. Recall that Christianity started with Jesus and a handful of his followers, with no great wealth, political power, or specialized scientific knowledge. Your effort must start with similarly humble circumstances. You cannot, for instance, enlist a billionaire to pay off the population of a whole city in some poverty-stricken country, to get them to act out a "resurrection" for your first set of witnesses. You cannot become the dictator of a country and force people to comply with your lies. You cannot impress some primitive, hidden tribe with modern science to get them to believe. You must play fair - using the same means that were available to the early Christians, if indeed their movement actually started naturalistically.
So, that is the challenge. You think you can fake a movement appearing to meet all of the above conditions? Go ahead and try. If you succeed, I will change my mind about the resurrection.
Conclusion
At last, we summarize this entire series.
First, we calculated the prior odds for the resurrection of Jesus Christ. This prior cannot be zero. That would violate one of the fundamental tenets of Bayesian thinking. Nor is a zero prior empirically justified, since we haven't actually observed an infinite number of people who didn't come back from the dead. Instead, empiricism requires this prior to be about the same as the reciprocal of the total number of non-resurrecting people we have observed, assuming we have observed zero resurrections. Rather generously, this could be placed at 1e-11 - roughly corresponding to observing the non-resurrection of the total number of humans that have ever lived.
Second, we calculated the Bayes factor for an earnest, insistent human testimony. Human testimony has value. This is not just an opinion or a hypothesis: human testimony must have value because your odds for an event actually changes when someone makes a testimony. Therefore, it must have a Bayes factor. The value of a human testimony can be thereby calculated on a mathematical and empirical footing. As it turns out, for an individual testimony like the ones appearing in Jesus's resurrection accounts, the Bayes factor is about 1e8. This is validated by multiple empirical observations, natural experiments, and thought experiments. There are several ways to modify this value depending on the exact nature of the testimony, which include things like dependency factors, incentives to lie, and the "stretchiness" of human testimony. All of these can be understood, and have been taken into account in the Bayes factor.
We next evaluated the amount of evidence for Jesus's resurrection. Just from the testimonies summarized in 1 Corinthians 15, we saw that six individuals or groups - Peter, James, Paul, the twelve disciples, the other apostles, and a crowd numbering more than 500 - all testified to Jesus's resurrection. Applying the Bayes factor calculated above - with the appropriate modifications - to this set of evidence gave an enormous total Bayes factor, easily enough to completely overwhelm the prior odds of 1e-11 against the resurrection. We therefore concluded that Jesus almost certainly rose from the dead.
This calculation was then double checked against other historical reports of a resurrection. By comparing against the non-Christian resurrection reports, we saw that the level of evidence behind Jesus's resurrection is a clear outlier, again to an absolutely overwhelming degree. This comparison therefore validated our earlier conclusion that Jesus rose from the dead.
Furthermore, because of the nature of this calculation, its conclusion is immune from many of the common skeptical arguments against the resurrection. The various possibilities - all the likely ways that the testimonies could have been wrong - have been already taken into account. No amount of speculation about how the resurrection reports could have been generated by naturalistic chance has any effect on the conclusion. We don't need to play 'what-if whack-a-mole' against the skeptic's "what about" speculations. This is a Bayesian argument. Speculations do absolutely nothing against it. Only evidence moves the odds.
However, because the Bayes factor for Jesus's resurrection is so large, we then had to start worrying about crackpot theories - conspiracies, vivid mass hallucinations, alien interference, and the like. At the level of certainty which was implied by our calculation, we had to take even such things into account. This required a recalculation, specifically to take into account every possibility, up to and including the near-total interdependency of evidence implied by such theories.
Fortunately, we have the historical data about other, non-Christian resurrection reports. This allowed us to explicitly and empirically construct the "skeptic's distribution", which is the probability distribution that generates the other historical resurrection reports through naturalistic means. This construction explicitly took into account the possibility of crackpot theories. This is the distribution that the skeptic must use, if they are to hold on to empiricism and naturalism - for this distribution incorporates the empirical, historical results of all such crackpot theories at the rate which actually occurred throughout history, and furthermore continues the distribution beyond the empirical end of the distribution using an exceedingly generous set of assumptions for the skeptic.
But even after taking even the crackpot theories into account, with a set of highly favorable assumptions for the skeptic, we saw that the Bayes factor for the testimonies for Jesus's resurrection still enough to amply overpower the 1e-11 prior odds. Combining this with the anti-crackpot defenses built into Christianity, we got a "final" probability for Jesus's resurrection of greater than 99.999%, as a very conservative estimate. So this recalculation again affirmed our previous conclusion: Jesus almost certainly rose from the dead, even when we consider all possible alternative theories.
But we did not stop there. As yet another test of our methodology, we used it to tackle a number of other, non-Christian, non-resurrection miracle stories. In each case we reached the reasonable conclusion - that probably nothing supernatural took place in these cases. It was a simple matter of quantifying the fact that the Christian miracles had ample evidence behind it, whereas the other miracles did not. Because this double-check reaches the same conclusions as the skeptic, the skeptic must therefore count this as an additional validation of the methodology.
(other double check)
But if anyone is still not convinced of Jesus's resurrection, I have the following challenge for them: naturalistically replicate the resurrection reports. Using the same means that were available to Jesus and his disciples - no political power, no great wealth, and no modern science - generate multiple, detailed, independent, earnest, insistent, enduring, and life-changing personal testimonies, from a great number of diverse types of people, unanimously testifying to a singular resurrection event. And this must be achieved in spite of deadly persecution, in a fractious movement with no central control, along with a host of other difficulties and conditions. If you still doubt Jesus's resurrection, the scientific method demands that you take up this challenge.
Alternatively, you can follow the logic of the methodology outlined above. It is based on mathematics and empirical data, has been validated and double-checked multiple times, and gives the correct answer in all cases where the answer could be agreed upon. Short of embracing epistemological obliteration, you must accept its conclusion: Jesus almost certainly rose from the dead.
Epilogue
As of April 2019, this work is now in its "third draft" form, although there are still whole sections that I need to add.
It all began as a post on March 21, 2016 - The week of Easter. When I started writing it, I only had the idea that you can actually calculate a value - a Bayes factor - for a human testimony. In a demonstration of my poor long-term planning skills, I initially just wanted to write that one post for Easter, about the likelihood of the resurrection based on the Bayes factor of the disciple's testimonies. But the ideas kept coming, they all required thorough explanations, and the posts just kept on writing themselves.
April 21, 2019 was the fourth Easter. In the year leading up to this date, I've refurbished a number of different arguments in the work. I feel that the broad strokes of the argument are fairly set at this point, even down to a number of details. I don't expect wholesale changes to the overall structure of the arguments, although smaller changes can still take quite some time to implement. The work will be released in an even more "public" release, with even stronger incentives for critical feedback.
First, I want to point out that in this whole time, I've never thrown out bad results or concealed disadvantageous conclusions. Every time a new idea came to me - every time there was a new way to test the veracity of the resurrection - I explored it, quantified the essential thoughts, thoroughly performed the necessary calculations, and presented the results. There were, of course, some thought branches that did not make it into the final work, but these were all because of reasons like the initial idea was mathematically unworkable, or the thought ended up being mistaken or redundant. Again, there was never a single instance where I reached a conclusion against the resurrection, and decided to hide or ignore it. There is no conscious selection or confirmation biases in this work. The resurrection was validated each and every time.
Second, I'd like to thank and acknowledge Aaron Wall of Undivided Looking for meaningfully affecting my thoughts and the shape of this work. He was of great help on a number of different subjects covered in this work, such as the handling of dependency factors and extreme odds values, and the "stretchiness" of human testimony.
I'd also like to thank the other people who have offered me feedback in private, who drove me to improve and solidify my work. If any of you remember talking to me about this, and would like a public acknowledgment here, just let me know!
Lastly, I'm again deeply thankful and gratified to have reached this next milestone, and I would appreciate your continued support and readership as I improve this work. And regardless of the time of the year, happy Easter to you all - Christ is risen indeed!
You may next want to read:
Leave a Reply
You must be logged in to post a comment.
Post Importance
Post Category
• humanities (26)
• current events (30)
• fiction (10)
• history (38)
• pop culture (14)
• frozen (8)
• math (58)
• personal update (21)
• logic (65)
• science (56)
• computing (16)
• theology (105)
• bible (40)
• christology (11)
• gospel (7)
• morality (23)
• uncategorized (2)