NaClhv

What is Bayesian inference? I've already mentioned it in several of my previous posts, and I'm sure to bring it up again in the future. I obviously think it's important. Why?

Bayesian inference is the mathematical extension of propositional logic using probability theory. It is superior to deductive propositional logic, which is what many people think of when they hear the word "logic". In fact it includes the rules of propositional logic as special cases of its more powerful and general rules. It is the logical framework that underlies the scientific method, and it encompasses a great deal of what it means to be a rational, logical, scientific individual. As with "normal", propositional logic, you don't necessarily have to be formally trained to use it in your daily life, but knowing its basics will greatly clarify your thoughts and sharpen your rational thinking skills. The intent of this post is to provide an introduction to this important topic.

Let's study an easy problem in propositional logic as a prerequisite review and a starting point for Bayesian logic. You should have learned in middle or high school that if A implies B, and B implies C, then A implies C. With some symbols, it becomes "if (A → B) and (B → C), then (A → C)". In an example with words, it might look like "If Socrates was a human, and all human are mortals, then Socrates was mortal". This is well and good. This is a fine way of thinking. Learning how to think this way is useful and worth learning.

However, when we examine the world around us, this rule is severely restricted in its applicability. Consider the following: "If Socrates was a human, and all humans have ten fingers, then Socrates had ten fingers". Is this sound? Can we conclude that Socrates necessarily had ten fingers? Well, no. The second premise - "all humans have ten fingers" - is not strictly true. Certainly most humans do, but not all. So we cannot conclude that Socrates had ten fingers. For that matter, we're not completely 100% sure that Socrates was human either.

"What's wrong with that?" You ask. "Hasn't logic brought us to a correct conclusion, that Socrates might not have had ten fingers?" True. But that's a very weak conclusion. Someone who was basing an argument on the possibility that Socrates didn't have ten fingers would need some additional evidence. I mean, until now I had implicitly assumed that Socrates had ten fingers, and I don't think I was being particularly irrational. Isn't there some way to conclude that "Socrates probably had ten fingers"? Maybe with a rule like "If A is likely to lead to B, and B is likely to lead to C, then A is likely to lead to C"? Doesn't that seem like a pretty logical conclusion?

Of course, "If A is likely to lead to B, and B is likely to lead to C, then A is likely to lead to C" is not a valid argument in propositional logic, and you can certainly find examples where A is true while C is not. For instance, "A blind person is likely to be a poor driver. Poor drivers are likely to get traffic tickets. Therefore, a blind person is likely to get traffic tickets" seems to be a incorrect chain of reasoning. But how could we be sure that it's not just an instance of bad luck, that this is just one of the cases where that probabilistic statement, "likely", just didn't pan out?

So we can't come to any firm conclusions about the "likely" rule in logic, although it seems to make sense sometimes. At any rate we can't use rigid propositional logic with such statements. But this is an enormous restriction, because there is nothing we know in the physical world with absolute certainty. Every instrument of measurement - including your own eyes and hands - are subject to errors and uncertainty. Even if you double check and verify, that only reduces the uncertainty to infinitesimal levels, without ever completely eliminating it. How can we reason in such cases - that is, in any real world scenarios where we are perpetually plagued by uncertainty?

In Bayesian reasoning, these uncertainties are built into its foundations. The truth of a statement is not represented by just "true" and "false", but by a continuous numerical probability value between 0 and 1. So, for instance, the statement "It will rain tomorrow" might get a probability value of 0.1, representing a 10% chance of rain. A statement like "I will still be alive tomorrow" might get a value like 0.999999, as I will almost certainly not die today. "1" and "0" would respectively correspond to absolute certainty in the truth or falsehood of a statement, but as I said they cannot be used in statements about the physical world. Instead we use numbers like 0.5 to represent the certainty that the coin will land heads, or 0.65 to represent the certainty you feel that you're going to marry that girl.

But isn't any given statement ultimately either true or false? Perhaps, but we are not God. We're ignorant of many things. But we still need to reason, even in our uncertainties. Giving a numerical, probabilistic truth value to a statement allows Bayesian reasoning to mirror the human mind much more closely than propositional logic. In essence, you can treat the numerical value you give to a statement as your personal degree of subjective certainty that the statement is true, given the information that you have.

But isn't this all very probabilistic, subjective, and uncertain? In one sense, yes. And that is a strength of Bayesian reasoning, because that's an actual limitation of the human mind. In representing the truth in this way we are only accurately representing how the truth actually exists in our minds. If we actually cannot be certain, then it's appropriate that our logical system actually represents that uncertainty.

But in another sense, this probabilistic thinking is completely rigorous and unyielding. By assigning a probabilistic value to the truth, you can use all of the mathematical tools of probability theory to process them, and their conclusions are mathematically certain. Bayesian reasoning makes very definitive statements about what these probability values must be, and how they must change in light of new evidence. I said earlier that Bayesian reasoning is an extension of logic using math, and that is exactly as rigorous and compelling as it sounds.

To finish this post, let me give you an extended example to illustrate both the rigor and flexibility of Bayesian reasoning, and its superseding superiority over propositional logic. We will address the question about Socrates and his fingers. There will be some math ahead, but nothing you can't understand at a high school level.

First, let me introduce some notations:

P(X) is the probability that you assign to statement X being true. So, if statement X is "I will roll a 1 on this dice", you might assign P(X)=1/6. But if you happened to know that the dice was loaded, you might assign P(X)=1/2 instead.

P(X|Y) is the probably that X is true, given that Y is already known to be true. So, if X is "It will rain tomorrow" and Y is "It will be cloudy tomorrow", then P(X) might only be 0.1, whereas P(X|Y) would be larger, perhaps something like 0.3. That is, there is only a 10% chance of rain tomorrow, but if we know that it will be cloudy, the chance of rain increases to 30%. Notice that the probabilities change depending on what additional relevant information is known.

This P(X|Y) notation is a little bit awkward, as it's written backwards from the more intuitive "if Y, then X" way of thinking. But unfortunately it's the standard notation. By definition, P(X|Y) = P(XY)/P(Y), where P(XY) is the probability that both X and Y are true.

~X is the negation of X. It is the statement that "X is false". By the rules of probability, P(~X)+P(X)=1, because X must be either true or false. Likewise, P(~X|Y)+P(X|Y)=1, and P(~XY)+P(XY)=P(Y)

You can translate a statement in propositional logic into a statement in Bayesian, probabilistic representation, simply by setting certain probabilities to 1 or 0. For instance, "X implies Y", which would be written as "X → Y" in propositional logic, would be written as "P(Y|X)=1" in terms of probabilities.

Now back to Socrates. Let the relevant statements be represented as follows:

A: "This person is Socrates"
B: "This person is a Human"
C: "This person has ten fingers"

Given these statements, we can translate the following statements as follows:

"Socrates was Human": P(B|A)
"Humans have ten fingers": P(C|B)

Now, let's show that we can duplicate the results of propositional logic simply by setting the probabilities to 1. If P(B|A) = P(C|B) = 1, then by the definitions given earlier, P(BA)=P(A), P(CB)=P(B), therefore P(~BA)=P(~CB)=0, therefore P(C~BA)=P(~CBA)=P(~C~BA)=0. But P(C|A) = [ P(CBA)+P(C~BA) ] / [ P(CBA)+P(C~BA)+P(~CBA)+P(~C~BA) ], which reduces to P(CBA)/P(CBA) =1 after eliminating all the zero terms. That is to say, if P(B|A) = P(C|B) = 1, then P(C|A) = 1. Or, translating back into words, "If Socrates is human, and humans have ten fingers, then Socrates has ten fingers".

Don't worry too much if you got lost in the notation in the above paragraph. The important point is that Bayesian reasoning can reduce down to propositional logic for the special cases where the probability values are set to 1 or 0. Bayesian reasoning thereby completely encompasses and supersedes propositional logic, like General relativity supersedes Newtonian gravity.

What if the probabilities are not 100%? This is the real-life problem of dealing with uncertainties. What is the actual value of P(B|A), the probability that Socrates was human? Might he not have been an alien, or an angel? As ridiculous as these possibilities seem, they ruin our complete certainty and makes propositional logic flounder. What about P(C|B) - the probability that a human has ten fingers? It's certainly not 100%. And what can we conclude about P(C|A) - the probability that Socrates had ten fingers?

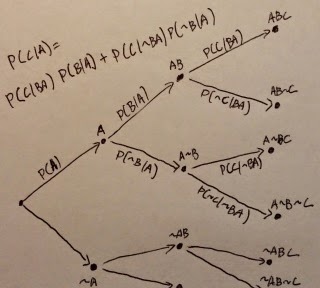
To tackle this question, we need to consider the following formula for P(C|A), which can be derived from straightforward application of the rules and definitions mentioned earlier. The fact that this formula exists - that we can actually derive it and use it to perform exact calculations - is one of the compelling fruits of the Bayesian way of thinking. Here it is:

P(C|A) = P(C|BA)P(B|A) + P(C|~BA)P(~B|A)

Let's say that Socrates has a P(B|A)=0.999 999 chance of being human, and that given all this, he has a P(C|BA)=0.998 chance of having ten fingers. This means that P(~B|A) = 0.000 001 is the chance that Socrates was not human. The last factor we need to know, P(C|~BA), is the probability that a non-human Socrates had ten fingers. This is nearly impossible to estimate, as we'd have to consider all the different things Socrates could have been - alien, angel, a demon in disguise, etc. But it will turn out not to matter much for our final result. Let's just assign P(C|~BA)=0.1. Plugging in the numbers and calculating, we get that P(C|A) = 0.997999102. That is to say, Socrates almost certainly had ten fingers.

If you want extra practice, you can also try using the formula on the "blind man getting traffic tickets" scenario above, and see why a blind man is not likely to get traffic tickets. Or you can wait until next week's post to get the answer.

But again, don't worry too much about the details of numerical calculation. The important point is that Bayesian reasoning provides an exact formula for calculating the probability of a conclusion, even when the premises were also only probabilities - which is always the case in the physical universe. Furthermore, the conclusions drawn this way are compelling, because they are mathematical results. If you accept the probabilities of the premises, then you must accept the conclusion. This is the same compelling force which is at work in propositional reasoning. The premises lead to inescapable conclusions.

I hope that this example demonstrates to you the usefulness of the Bayesian way of reasoning. It can be actually applied to situations with uncertain premises, which is really nearly all situations. It is completely rigorous in that a correct Bayesian argument forces you to accept its conclusions if you accept its premises. Yet it's also flexible in assigning probabilities to reflect your current, subjective, personal degree of belief in the truthfulness of a statement. It duplicates propositional logic as its special cases, and in its full form it's more general and more powerful than propositional logic. There are other advantages I have not yet touched on, such as its ability to naturally explain inductive reasoning and Occam's razor, and how it serves as the framework for the scientific method. On the whole, it encompasses a great deal of what it means to be a logical, rational, and scientific thinker.

In my next post, I will discuss a particularly important formula in this probabilistic way of thinking, one that is nearly synonymous with Bayesian reasoning - Bayes' theorem.

You may next want to read:
Basic Bayesian reasoning: a better way to think (Part 2) (Next post of this series)
What is "evidence"? What counts as evidence for a certain position?
Miracles: their definition, properties, and purpose
Another post, from the table of contents