NaClhv

Recall that we're constructing a "skeptic's distribution" - the probability distribution of generating a resurrection report with a certain level of evidence. We will construct it from historical, empirical data. This allows us to bypass the mess of trying to compute everything from first principles, and ensures that the this is the correct distribution - a skeptic cannot reject it without rejecting history or empiricism.

So, what form should this "skeptic's distribution" take?

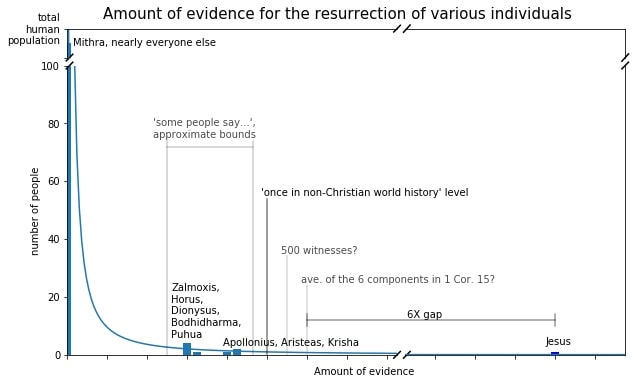
How about using a normal distribution? Well, that would be plainly ridiculous. The data we have thus far has Jesus (very conservatively) having 24 times more evidence for his resurrection than anyone else in history. Our goal is to get the probability for something like this happening.

But if we used a normal distribution for the "skeptic's distribution", this could essentially never happen. Recall that human heights roughly follow a normal distribution. Then, our problem would be analogous to looking for someone 24 times taller than anyone else in history - that is, someone well over 200 feet tall. The probability for something like that is essentially zero. So if we chose the normal distribution, we'd essentially be dooming the skeptic's case from the start.

The same is true for an exponential distribution. An exponential distribution decreases in its probability value by a constant factor for each unit of increase in its domain. As the domain is "level of evidence" in our problem, this means that each piece of evidence would multiply the probability values. That is to say, we'd be treating each piece of evidence independently. And we already saw that even with a reasonable degree of dependence factored in, the probability values already reached numbers like 1e-54, again dooming the skeptic's case.

This is a testament to how quickly these distributions decay as they extend to the right. Their right tails are so "stubby" that the maximum values of their samples are strongly restricted, and getting something 24 times greater than that maximum is essentially impossible. Picking any such distribution would not be taking into account the dependence of the evidence, and would unfairly doom the skeptic's case from the start.

Rather, we need a distribution with a "long tail" - something that has a chance for a new high record to beat the previous record by factors like 24. Something that decays slowly enough that its probability values remain non-negligible as we move further to the right. The distribution should still be realistic and have some justification for being selected, but we want to give the skeptic the best chance.

Taking all that into account, I have chosen a power law function for the "skeptic's distribution". This should not be a surprise - indeed anyone familiar with the statistics of human behavior might have guessed it from just the histogram we're trying to fit:

What makes a power law particularly appropriate? Well, for one, power laws are the quintessential long-tailed distribution. They have one of the longest possible tails, and are fully "capable of  black swan behavior", according to Wikipedia. They can easily have tails so long that the overall distribution has an undefined (that is, infinite) mean. In fact, power laws, as mathematical functions, can decay so slowly that it's not allowed to be a probability density function, because the area under their curve can diverge. One can hardly ask for a more slowly decaying function than that. So this gives the skeptic the best chance at naturally generating a Jesus-level of resurrection evidence.

There exists distributions that decay even more slowly than a power law, but they're rare, obscure, and have no relation to what we're doing. By contrast, power law distributions are ubiquitous in human behavior. They form the basis for the well-known Pareto principle, and they capture the "dependency of evidence" factor we're currently trying to model.

For example, the distribution of income among people follows a power law. A few people, out at the long tail, have a great deal of wealth, because rich get richer - that is, because how rich you get depends on how rich you already are.

The size of cities also follows a power law. There are a few very large cities out at the long tail, because your chances of moving to a city depends on the number of people who already live there.

The number of links to a website follows a power law. There are a few, very popular websites out at the long tail, which have a lot of links to them. This is because a site's chances of getting a link depends on its popularity - that is, on the number of links it already has.

Don't let the specificity of these examples fool you. There are many, many more. Power law distributions are, as I said, ubiquitous in human behavior. They will frequently come up when one human behavior depends on the same kind of behavior, either by others or by the same person.

So it is entirely appropriate that we use a power law to  model the level of evidence for a resurrection report. There will be relatively few reports out at the long tail, like the "resurrection" of Apollonius or Krishna. In the context of things like conspiracy theories, this is because the chances of generating an additional piece of evidence depends on how much evidence it already has.

So there are excellent external reasons and examples to expect that the "skeptic's distribution" will follow a power law. Furthermore, power laws give one of the best possible chances for the skeptic's case, having a very "long tail" and allowing for a "black swan" event like the level of evidence in Jesus's resurrection event.

We will proceed to nail down the specifics of this power law distribution in the next post.