NaClhv

We've decided on a power law as the general form of the "skeptic's distribution".

The details of the distribution near zero will not particularly matter. We're more concerned about how rapidly it decays at very large values. This allows us quite a bit of leeway in choosing the specific form of the power law distribution, as they all decay similarly as we move along the tail off to the right.

For this reason, I've chosen the generalized Pareto distribution as the specific form of the "skeptic's distribution", guided chiefly by the straightforward interpretation of its parameters. But the choice here will not affect any conclusions. Any other power law distribution would give the same results.

The generalized Pareto distribution is characterized by three parameters: location, scale, and shape. The location parameter determines where the distribution starts. It's where the probability density of the distribution is the largest. As the vast majority of humans have zero evidence suggesting that they rose from the dead, the location parameter should obviously be set at zero.

The scale parameter is irrelevant; it only controls how far the distribution should multiplicatively scale in the horizontal direction, and can be arbitrary changed by changing the unit of evidence we use. As we'll consider all the evidence for our the resurrection reports relative to one another (for example, as a fraction of the amount of evidence for Christ's resurrection), the value for the amount of evidence in some specific units never enters the picture. So we'll just set this parameter to 1, or to whatever is convenient for visualization, and forget about it.

The shape parameter is the interesting one. It's what we really care about. It effectively determines the power in the power law, and controls how quickly the function decays as the amount of evidence increases.

For example, this is what the tail end of the distribution looks like with various shape parameters:

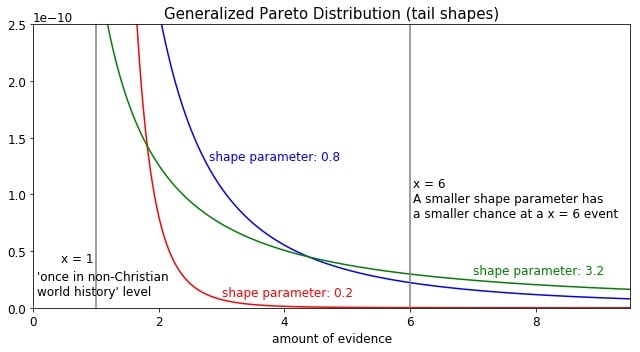
In each case, the distribution has been scaled so that the total probability to the right of the grey line (at x=1) is 1e-9. Essentially, x = 1 is where you would expect the maximum value out of 1e9 samples to appear, corresponding to the level of evidence for the resurrection of a figure like Apollonius or Aristeas.

Note the different rates decay. With the shape parameter at 0.2, the probability density drops to practically zero as we move to larger x values. There is essentially nothing left by the time we've moved to x = 24, even if we integrate out to infinity. Therefore, if this were the final form of the "skeptic's distribution", the probability of generating a Jesus-level of evidence for a resurrection would be essentially zero.

However, with the shape parameter at 2, we see that the decay rate is much slower, and there is a good amount of probability even out at x = 24 and beyond. If this were the "skeptic's distribution", it would have a good chance of generating a Jesus-level of evidence for a resurrection, even if that level were 24 times higher than the runner-up.

A shape parameter of 20 decays more slowly still. It's hardly decaying at all by the time it reaches x = 24. In fact, it decays so slowly that the blue curve with the shape parameter of 2 will eventually move below it. If this were the "skeptic's distribution", it would have a non-negligible chance of generating an event at x values of much higher than 24.

So, it all comes down to the shape parameter. But how shall we decide on its value? Why, by choosing the one that best fits the data according to Bayes' theorem, of course.

We will outline this procedure in the next post.