How to think about the future (Part 3)
It's easy to predict the future. It'll be basically like the past.
How could that be? Isn't everything changing all the time? Are we not living in an era of unprecedented growth and technological advancement? Isn't the world not only changing, but changing faster and faster? I mean, just look at the graph of the world population: look at that absolute explosion in recent years. And similar graphs can be made for technological progress as well. Isn't it absolutely clear that the present is completely different than the past, that we are on the cusp of something disastrous or transcendent, and that the future will be far more different still?
Well, in a sense, I guess that's true. But that's pretty much always been true. That's what I mean by saying the future will be like the past. All those hyperbolic things said about the future could have been said at most other times in the past - A hundred, two hundred, or perhaps even thousands of years ago. And they would have been about as right then as we are now in saying these things. That is simply the nature of exponential growth.
Here's what I mean: if we assume that humanity's growth - whether it's measured in population or in technological development - follows an exponential curve, then the future can always be exactly mapped onto the present, or the past, through some simple transformations. Let me demonstrate: consider the following graph:
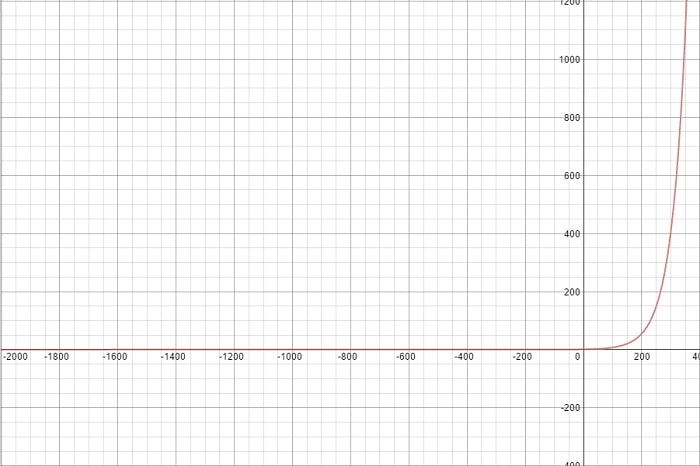
That exponential graph may represent world population or technological growth or whatever. Isn't it clear that there are two distinct regions in that graph, the flat region and the rapid rise before the end? Let's zoom in to the transition between the two regions:
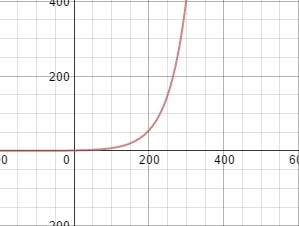
Isn't that where we are in history? At that unique and crucial point where we leave off being "flat" to where everything blows up and goes off the scale?
Well, let's not do anything hasty based on that line of thinking. After all, I can make any other region of the graph look exactly like that "unique and crucial point" by simply focusing on that new point and re-normalizing the y-axis. The following is a graph of the exact same function as before at a different x-value, viewed according to the treatment I just prescribed:
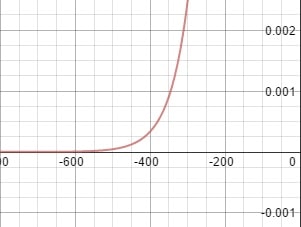
Note that the view window is now focused around -400 instead of +200, and the y-axis has been re-scaled. But the shape of the function is exactly the same as it was before. You can try this for yourself - desmos is a good online graphing calculator - and see that it's true, starting with any exponential growth function. Algebraically, this is because if you
1. take any exponential function (e^kx),
2. and translate it horizontally by any amount (e^k(x+x0)),
3. and vertically scale it to re-normalize things so that the new y-value becomes the new normal ( 1/e^kx0 * e^k(x+x0))
4. then you get back your original function. (e^kx)
This means that if you transport yourself to any time in history, and get used to your environment so that this new time period becomes your new "normal", then the pace of the changes around you will look the same as it does now. In fact, it'll look the same at any other time in history. There is therefore nothing new under the sun, and the future will be like the past.
You can even test this with events within living memory. Consider that archetypal example of modern progress: the advancements in computers. Back when I first started to really look at computers, a "gigabyte" was an unheard amount of storage for a computer to have. If you had told me then of a future of such rapid progress where a computer's storage increased by many gigabytes in a couple of years, I might have marveled at this hyper-technological future where such wonders were possible. I might have thought that everything I knew would be thrown out and be completely changed in this new world. But of course, this is the future we live in now, and the increase from 64 to 128 GB between iPhone 5 and 6 is not some world-shattering news.
Now, one may argue that the pace of growth has actually been even faster than merely exponential growth - there may be something to be said for that. Certainly, this graph of the world's population has distinct regions, and the growth is not only exponential, but there are period where the exponential growth rate itself increases. But I think it's too much to conclude that this is the definitive, continuous pattern in human progress. I think that the graph can be best interpreted by saying that human growth rate is usually exponential, but that at the rate of growth jumps to a new value at certain moments in history (the beginning of civilization, the industrial revolution, etc). We may be in such a moment in history, but even so, the rate of change would not be fundamentally different than they were during the industrial revolution. It's exciting, to be sure, but it's not the end of the world, and the future will continue to be more or less like the past.
.png){kind=link}
You may next want to read:
How to think about the future (Part 4) (Next post of this series)
How to think about the future (Part 2) (Previous post of this series)
How to make a fractal
Another post, from the table of contents
One comment on “How to think about the future (Part 3)”
Leave a Reply
You must be logged in to post a comment.
Broadly speaking, yes. The past and the future are linked in ways that make predictions straight-forward. Of course, assuming that the past and the future MUST be just like the present is equally fallacious as assuming they are not; for instance, naively extrapolating backward from exponential growth would prove that at some point in the distant past, there were approximately 0.718 people on this planet, which of course makes no sense. Even leaving aside the ridiculous, there are plenty of factors that mean we mustn't assume too much constancy. But generally speaking, this is exactly what we do every day to try to make expectations about the future, and what we equally do every day to make deductions about the past.